이번에는 생성한 그래프에서 두 정점 간의 최대 유량을 계산하는 알고리즘을 구현하였다.
최대 유량 문제란, 용량이 주어진 간선에 대해 최대 유량을 구하는 문제를 의미한다.
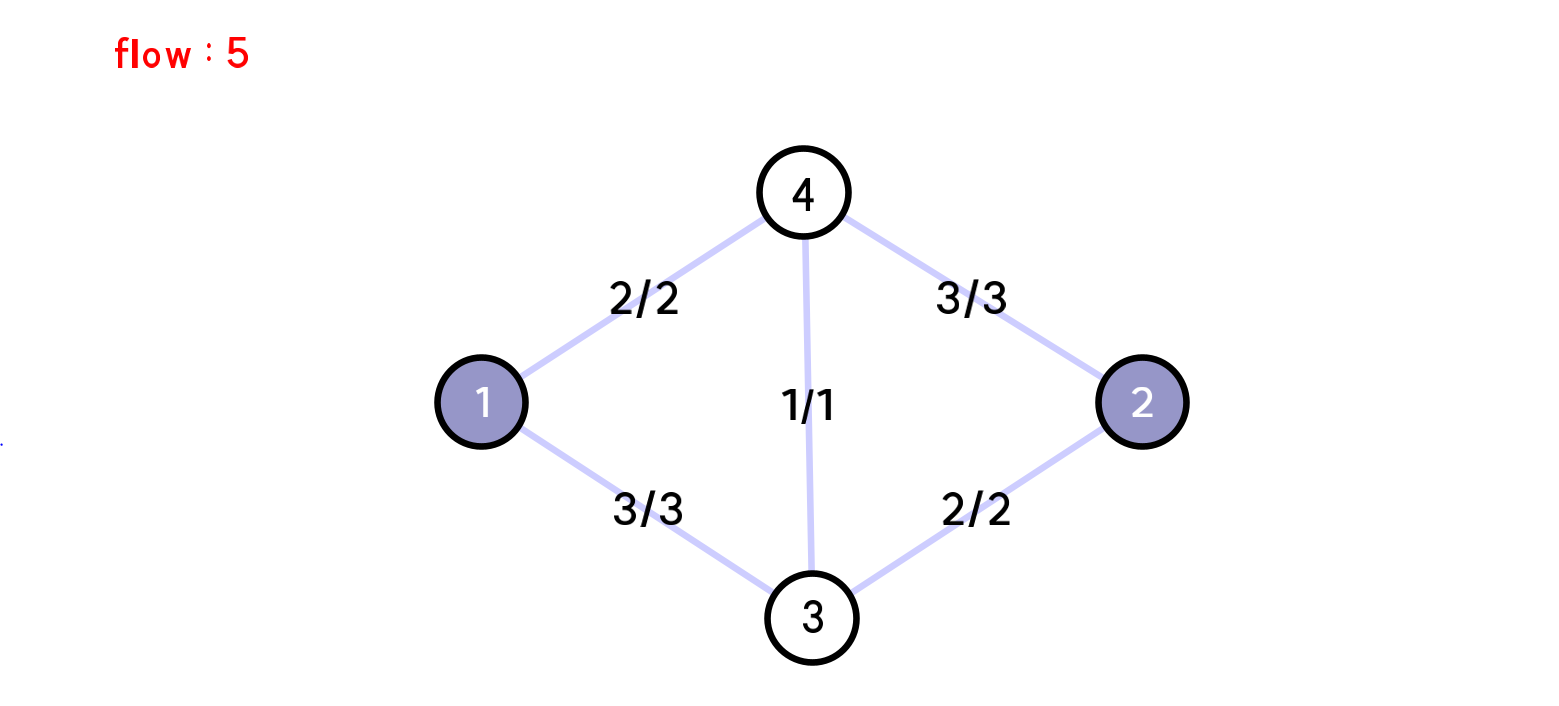
다음과 같이 그래프가 주어진 상황을 가정하면,

1 → 3 → 4 → 2로 1의 유량을 흘려주고,
1 → 4 → 2로 2의 유량을 흘려주고,
1 → 3 → 2로 2의 유량을 흘려주면 총 5의 유량을 보낼 수 있다.
최대 유량 알고리즘으로는 에드몬드-카프 (Edmonds-Karp) 알고리즘을 사용하였다.
시간복잡도는 $O(VE^{2})$으로, 돌아가기에는 충분한 알고리즘이기에 이를 활용하였다.
두 지점을 연결하는 어떠한 경로에 대해 유량을 흘려줄 수 있다면, 항상 흘려주는 것이 더 이득이다.
즉, 그리디하게 문제를 해결할 수 있다.
만약 이 방법을 사용하여 더 많은 유량을 흘려줄 수 있는 방법을 쓸 수 없게 되었다고 가정한다면,
해당 두 방법의 각각의 경로에 대해 반드시 같은 노드를 사용하는 구간이 존재한다.
그렇지 않다면 두 경로는 전혀 영향을 주지 않기 때문에, 맨 처음의 가정에 모순이다.
이때, 먼저 흘려준 양을 s라 하고, 나중에 흘려준 양을 e라고 한다면,
공통된 노드에 대해 적어도 e의 유량을 흘려줄 수 있었으므로, 앞으로도 최소 e-s의 유량을 흘려줄 수 있다.
이제 e-s의 유량을 기존의 e를 흘릴 수 있던 방법에 흘려준다면 e의 유량을 얻을 수 있다.
따라서 더 많은 유량을 흘려줄 수 있는 방법을 쓸 수 없었다는 가정이 모순이 되므로 처음 가정이 성립한다.
여기서 사용한 알고리즘은 에드몬드-카프 알고리즘으로, BFS 기반으로 경로를 계속해서 찾아 탐색하는 방법이다.
시간 복잡도는 $O(VE^{2})$이다.
먼저, BFS를 활용하기 위한 큐 자료구조를 구현해 주었다.
간단하게 Circular Queue를 구현하여 활용해 주었다.
//queue
int mod = 200;
int []queue = new int[201];
int s = 0,e = 0;
void push(int data)
{
queue[e] = data;
e = (e + 1) % mod;
}
int front()
{
if(s == e) return 0;
int res = queue[s];
s = (s + 1) % mod;
return res;
}
boolean empty() { return s == e ? true : false; }
void q_reset()
{
for(int i=0;i<=200;i++) queue[i] = 0;
s = 0; e = 0;
}
다음으로, 에드몬드-카프 알고리즘을 구현할 것이다.
위에서 그리디가 성립한다는 것을 보였으므로 계속해서 가능한 간선에 유량을 반복적으로 흘려주면 된다.
이때, 네트워크 플로우 알고리즘의 핵심으로, 어떠한 간선에 유량을 흘려주었다면,
반대 방향의 간선에는 음의 유량을 흘려주어 역방향으로 탐색이 가능하게 진행해 주어야 한다.
그래프가 방향 그래프일 경우 단방향 간선에 대하여 반대 방향으로는 가중치가 0인 가상의 간선으로 간주하고 해결하였지만,
현재는 양방향 그래프일 경우를 가정하고 구성하였으므로 반대 방향으로도 동일한 가중치를 두어 해결할 수 있다.
소스 코드는 다음과 같다.
int []parent = new int[101];
int source = 1, sink = 2;
int flow()
{
int res = 0;
while(true)
{
for(int i=1;i<=100;i++) parent[i] = -1;
s = e; //queue reset
parent[source] = source;
push(source);
while(empty() == false && parent[sink] == -1)
{
int cur = front();
for(int nxt = 1; nxt <= 100; nxt++)
{
if(nxt == source) continue;
if(capacity[cur][nxt] > flow[cur][nxt] && parent[nxt] == -1)
{
parent[nxt] = cur;
push(nxt);
}
}
}
if(parent[sink] == -1) break;
int amount = 10000000;
for(int cur = sink; cur != source; cur = parent[cur])
{
int prv = parent[cur];
amount = min(amount, capacity[prv][cur] - flow[prv][cur]);
}
for(int cur = sink; cur != source; cur = parent[cur])
{
int prev = parent[cur];
flow[prev][cur] += amount;
flow[cur][prev] -= amount;
}
res += amount;
}
return res;
}
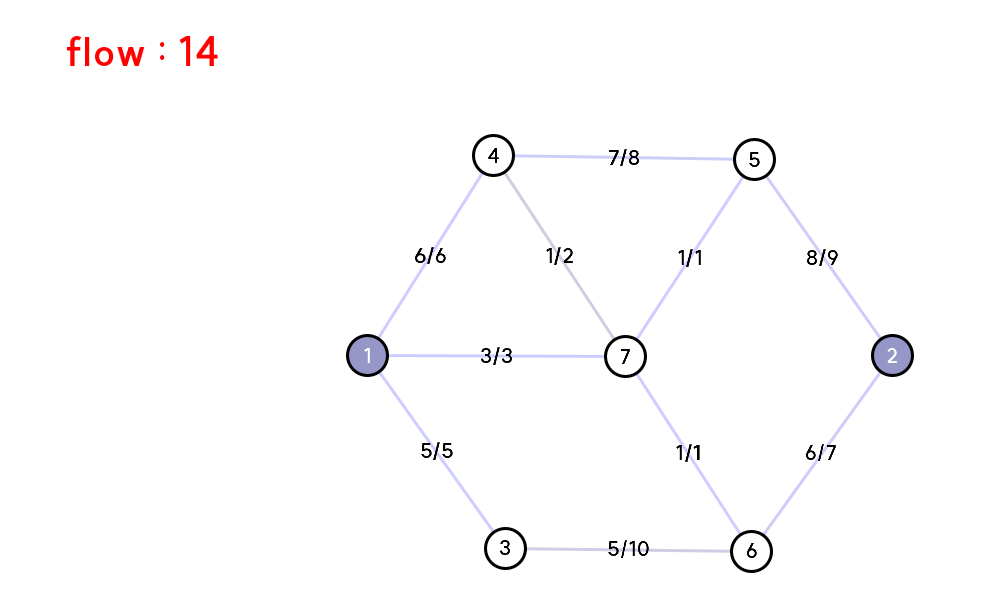
마지막으로 그래프 시스템을 조금 수정해준 후, 알고리즘을 실행시켜 주었다.
네트워크 플로우 알고리즘의 경우 알고리즘이 끝난 후의 유량은 곧 최적의 해를 의미하기 때문에 이를 출력해 주었다.
이때 간선 용량에 대한 최적의 해일 때의 유량의 비율로 색상을 표현하였다.
아래는 임의로 구성한 그래프와 그에 따른 알고리즘 실행 결과이다.

향후 계획
실행 결과 간선에 어떤 방향으로 유량이 흐르는 지 직관적으로 파악하기 어렵기 때문에, 이를 개선할 것이다.
또한, 실제 데이터를 불러와 그래프를 구성할 수 있도록 기능을 추가할 것이다.
'과학고 조기졸업 과제 > 정보과학 융합탐구' 카테고리의 다른 글
| Network Flow를 활용한 그래프 시뮬레이터 제작 (0) | 2024.04.03 |
|---|---|
| 네트워크 플로우를 활용한 그래프 시뮬레이터 제작 (3) (0) | 2024.04.02 |
| 네트워크 플로우를 활용한 그래프 시뮬레이터 제작 (1) (0) | 2024.03.26 |
| 네트워크 플로우를 활용한 그래프 시뮬레이터 제작 계획 (0) | 2024.03.26 |