문제 링크
https://www.acmicpc.net/problem/16404
16404번: 주식회사 승범이네
첫 번째 줄에 승범이를 포함한 판매원들의 수 N(1 ≤ N ≤ 100,000), 명령의 수 M(1 ≤ M ≤ 100,000)이 주어진다. 판매원들은 1번부터 N번까지 번호가 매겨지며, 승범이는 항상 1번이다. 두 번째 줄에 판
www.acmicpc.net
문제 선정 과정
서브트리 전체의 값에 업데이트를 해야 하는데, 제한을 보니 이를 $logN$에 끝내야 하는 것으로 보였습니다.
그냥 배열로도 단순히 풀면 나오지 않는 시간 복잡도인데 이를 트리에서 시행해야 한다는 점에서 꽤나 어려운 문제라 생각했습니다.
문제 풀이 전략
문제를 모델링하면 다음과 같습니다.
- 정점이 N개인 트리에 다음 두 가지 쿼리가 주어집니다.
- 쿼리 1: i를 루트로 하는 서브트리 내의 모든 정점에 w를 더합니다.
- 쿼리 2: 정점 i의 값을 출력합니다.
구간 업데이트가 빈번히 일어난다는 점에서 Lazy Propagation을 활용한 Segment Tree를 써야겠다는 생각이 들었습니다.
자료 구조
Segment Tree는 구간에 대한 정보를 빠르게 얻기 위해 만들어진 자료 구조입니다.
분할 정복의 과정들을 노드에 담아 저장하는 방법으로 구현되어 있습니다.
예를 들어, 배열 [1, 4, 5, 8] 의 구간 합을 세그먼트 트리로 저장하면 다음과 같이 구성됩니다.
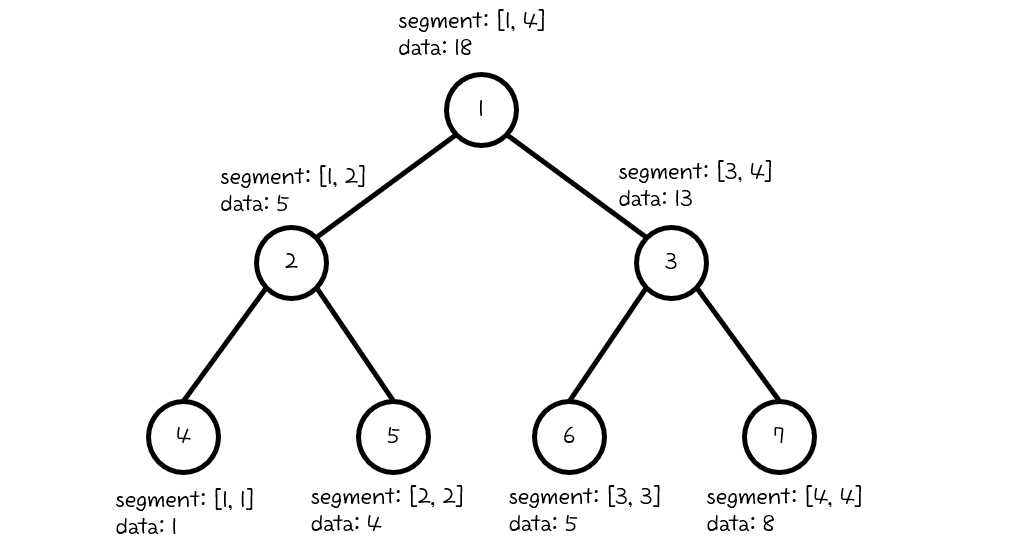
세그먼트 트리의 장점은 이진 트리를 기반으로 구성되기 때문에, 높이가 최대 $logN$이 됩니다.
어떤 데이터가 갱신된다면, 그 데이터를 가지고 있는 구간은 총 $logN$개이기 때문에, 이들만을 갱신하면
시간 복잡도가 $log N$이 됩니다.

또한 어떤 구간에 대한 정보를 얻는 경우에도, 구간을 계속 반으로 나누어 구하므로 $logN$개만의 데이터로 구성할 수 있습니다.

그러나 구간 전체에 대한 업데이트가 주어진다면, 데이터를 하나씩 갱신하기에는 시간이 너무 오래 걸립니다.
이때, 구간 쿼리가 들어오기 전이고, 현재까지 변경될 값의 데이터를 알고 있다면,
이를 필요할 때만 업데이트하여 시간 복잡도를 크게 줄일 수 있습니다.
이를 Lazy Propagation이라 부릅니다.


그림과 같이 구간 [1, 2]에 대한 lazy 값은 아직 요구되지 않았기 때문에 남아있는 모습을 확인할 수 있습니다.
이렇듯 매번 업데이트를 진행하지 않고, 꼭 필요할 때만 업데이트를 하는 방식으로 진행한다면
전파 과정의 시간복잡도 $O(logN)$, 구간 처리 과정 $O(logN)$으로 총 $O(logN)$으로 해결할 수 있습니다.
이제 문제를 해결해 봅시다.
그러나 트리는 비선형 자료구조이기 때문에, 세그먼트 트리를 활용하기 위해서는
선형 자료구조로 접근할 수 있도록 해주어야 합니다.
이는 Euler Tour Technique이라 불리는 방법으로 변환이 가능합니다.
트리에서 DFS를 돌리며 노드별로 번호를 매기고, 서브트리 내에서 처음으로 방문된 노드부터 마지막으로 방문된 노드까지의 구간은
곧 서브트리 전체에 대한 접근을 의미하게 됩니다.
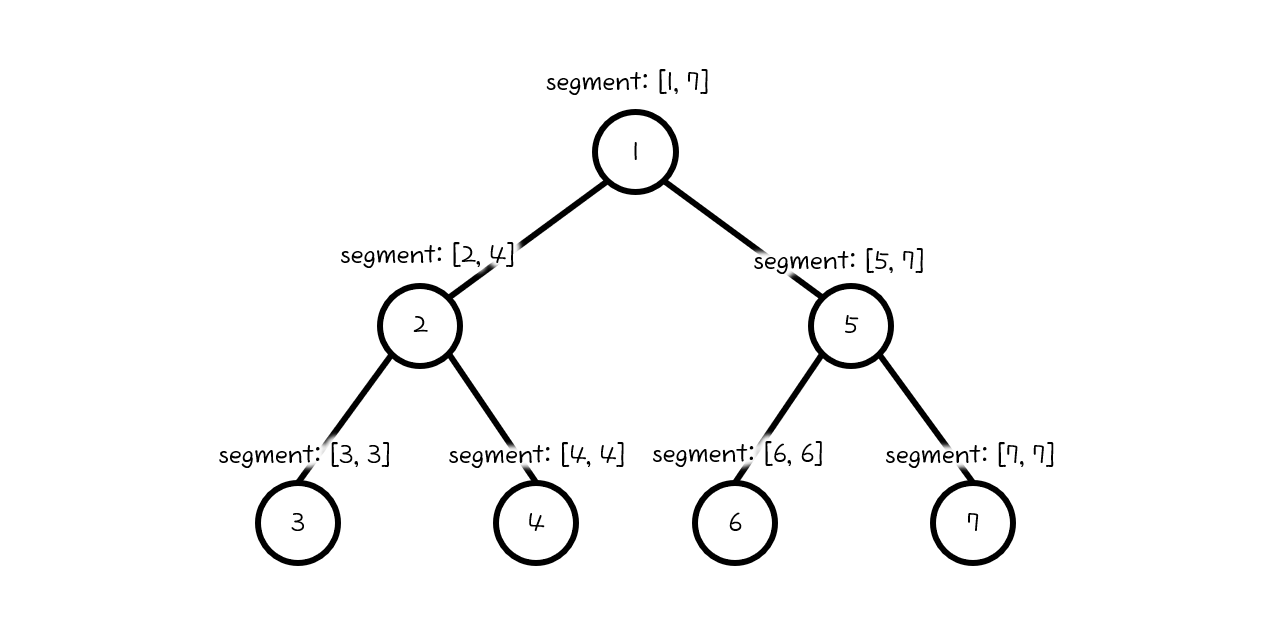
이제 각각의 서브트리의 루트 노드가 담당하는 구간을 세그먼트 트리로 관리해준다면 문제를 해결할 수 있습니다.
먼저 생성된 그래프에 대해 노드별로 번호를 매기는 과정입니다.
#include <iostream>
#include <vector>
using namespace std;
typedef long long int LL;
vector<int> node[100001];
int cnt = 1;
int s[100001], e[100001];
void tour(int cur, int parent)
{
s[cur] = cnt;
cnt++;
for(auto nxt: node[cur])
{
if(nxt == parent) continue;
tour(nxt, cur);
}
e[cur] = cnt - 1;
}
다음으로 Lazy Propagation을 활용하여 세그먼트 트리를 구성하는 과정입니다.
Propagate 함수는 Lazy 값을 자식 노드에게 전파하는 함수입니다.
매 업데이트와 쿼리가 들어올때만 실행시켜 시간복잡도를 줄일 수 있습니다.
LL tree[400001];
LL lazy[400001];
void propagate(int node, int s, int e)
{
if(lazy[node] == 0) return;
tree[node] += (e - s + 1) * lazy[node];
if(s != e)
{
lazy[node * 2] += lazy[node];
lazy[node * 2 + 1] += lazy[node];
}
lazy[node] = 0;
}
LL update(int node, int s, int e , int l, int r, LL w)
{
propagate(node,s,e);
if(e < l || r < s) return tree[node];
if(l <= s && e <= r)
{
tree[node] += (e - s + 1) * w;
if(s != e)
{
lazy[node * 2] += w;
lazy[node * 2 + 1] += w;
}
return tree[node];
}
int m = (s + e) / 2;
LL L = update(node*2,s,m,l,r,w);
LL R = update(node*2+1,m+1,e,l,r,w);
return tree[node] = L + R;
}
LL query(int node, int s, int e, int l, int r)
{
propagate(node,s,e);
if(e < l || r < s) return 0;
if(l <= s && e <= r) return tree[node];
int m = (s + e) / 2;
LL L=query(node*2,s,m,l,r);
LL R=query(node*2+1,m+1,e,l,r);
return L + R;
}
아래는 전체 풀이입니다.
쿼리 $M$개에 대해 시간복잡도가 $O(logN)$이므로 총 시간복잡도는 $O(MlogN)$입니다.
#include <iostream>
#include <vector>
using namespace std;
typedef long long int LL;
vector<int> node[100001];
int cnt = 1;
int s[100001], e[100001];
void tour(int cur, int parent)
{
s[cur] = cnt;
cnt++;
for(auto nxt: node[cur])
{
if(nxt == parent) continue;
tour(nxt, cur);
}
e[cur] = cnt - 1;
}
LL tree[400001];
LL lazy[400001];
void propagate(int node, int s, int e)
{
if(lazy[node] == 0) return;
tree[node] += (e - s + 1) * lazy[node];
if(s != e)
{
lazy[node * 2] += lazy[node];
lazy[node * 2 + 1] += lazy[node];
}
lazy[node] = 0;
}
LL update(int node, int s, int e , int l, int r, LL w)
{
propagate(node,s,e);
if(e < l || r < s) return tree[node];
if(l <= s && e <= r)
{
tree[node] += (e - s + 1) * w;
if(s != e)
{
lazy[node * 2] += w;
lazy[node * 2 + 1] += w;
}
return tree[node];
}
int m = (s + e) / 2;
LL L = update(node*2,s,m,l,r,w);
LL R = update(node*2+1,m+1,e,l,r,w);
return tree[node] = L + R;
}
LL query(int node, int s, int e, int l, int r)
{
propagate(node,s,e);
if(e < l || r < s) return 0;
if(l <= s && e <= r) return tree[node];
int m = (s + e) / 2;
LL L=query(node*2,s,m,l,r);
LL R=query(node*2+1,m+1,e,l,r);
return L + R;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
int n,m;
cin >> n >> m;
for(int i=1;i<=n;i++)
{
int t;
cin >> t;
node[t].push_back(i);
node[i].push_back(t);
}
tour(1, -1);
int mx = -1;
for(int i=1;i<=n;i++) mx = max(mx, e[i]);
while(m--)
{
int num,i;
LL w;
cin >> num;
if(num == 1)
{
cin >> i >> w;
update(1,1,n,s[i],e[i],w);
}
else
{
cin >> i;
cout << query(1,1,n,s[i],s[i]) << '\n';
}
}
}
느낀 점
세그먼트 트리와 Lazy Propagation을 적절히 응용할 수 있는 좋은 문제였던 것 같습니다.
또한 그래프에 번호를 매겨 이를 세그먼트 트리로 관리하는 아이디어가 굉장히 인상 깊었습니다.
'과학고 조기졸업 과제 > AP 프로그래밍과 문제해결' 카테고리의 다른 글
| 5. Discrete Convolution (0) | 2024.03.26 |
|---|---|
| 4. RPG Extreme (0) | 2024.03.21 |
| 2. 교수님은 기다리지 않는다 (1) | 2024.03.14 |
| 1. 잔디밭과 개미굴 (0) | 2024.03.14 |