문제
https://judge.codingpanda.kr/problem.php?id=1761
Discrete Convolution - 문제 - CodingPanda
합성곱 (Convolution)은 신호 및 시스템, 디지털 처리 등 다양한 분야에서 쓰인다. 특히 인공지능 쪽으로는 합성곱 신경망 (Convolution Neural Network, CNN)에 응용되는 개념이다. 두 벡터 A,B에 대해, 이산
judge.codingpanda.kr
문제 제작 과정
알고리즘들을 배우면서 실제로 사용되는 분야에 적용시켜 문제를 만들고자 하였습니다.
따라서 인공지능 분야의 합성곱 신경망 (Convolution Neural Network, CNN)에 사용되는
합성곱 알고리즘을 구성하는 문제를 제작하게 되었습니다.
배경지식
두 벡터의 이산 합성곱 연산은 다음과 같이 정의됩니다.
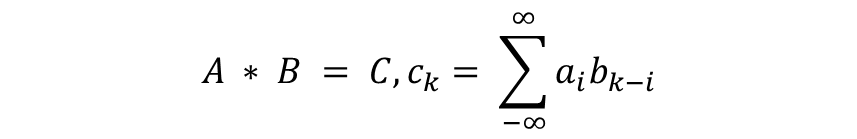
이를 Naive하게 구성해 준다면 $O(N^{2})$로 해결할 수 있으나, 이는 단순 반복 연산으로 해결 가능합니다.
따라서 알고리즘을 활용할 수 있도록 N <= 100000으로 구성해 주었습니다.
이때 고속 푸리에 변환(Fast Fourier Transform, FFT)을 활용해 준다면 $O(NlogN)$으로 해결할 수 있습니다.
먼저 이산 푸리에 변환은 다음과 같이 정의합니다.
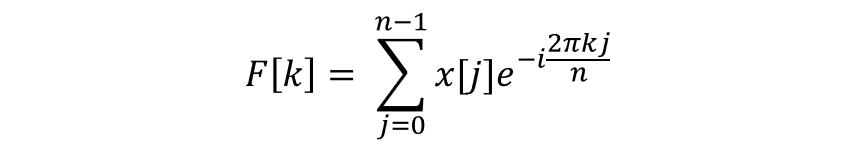
푸리에 변환은 다양한 분야에서 사용되나, 여기서 푸리에 변환의 사용 이유는 2가지입니다.
먼저 역변환이 굉장히 간단합니다.
역변환은 굉장히 잘 정의되어 있기 때문에, 단순한 연산으로 충분히 해결 가능합니다.
다음으로 두 벡터의 합성곱은 두 벡터에 각각 DFT를 취해준 후, 내적해주어 역변환시켜준 것과 동일합니다.
따라서 DFT의 시간 복잡도를 줄이는 방법으로 시간 복잡도를 향상시킵니다.
이산 푸리에 변환에서 가장 널리 사용되는 Cooley-Tukey Algorithm은 벡터의 크기가 2의 거듭제곱일 때만 사용 가능하나,
임의의 벡터에 대해서 강제로 크기를 바꾸어 주면 되기 때문에 별다른 문제는 존재하지 않습니다.
예를 들어 N=4일 때, 다음과 같은 벡터가 존재한다고 하면,
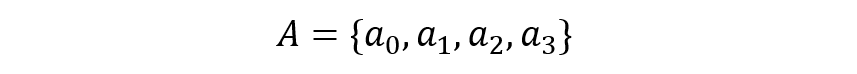
이산 푸리에 변환을 거친 벡터는 다음과 같습니다.

그러나 이 역시 Naive하게 구현하면 시간 복잡도가 $O(N^{2})$입니다.
이때 다음과 같이 짝수 번째 원소와 홀수 번째 원소를 분리하여 따로 벡터를 생성해주는 것을 생각해볼 수 있습니다.

이때 각각의 벡터에 대해 푸리에 변환을 시행해주면 다음과 같은 벡터를 얻을 수 있습니다.

이 두 벡터를 결합하여 전체 벡터에 대한 푸리에 변환을 얻을 수 있습니다.
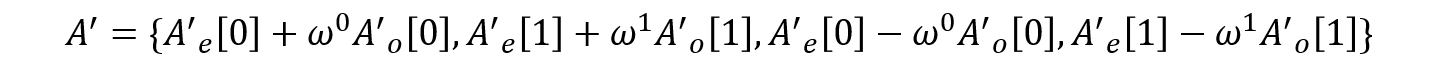
이를 일반화하면 다음과 같습니다.

이러한 방법으로 분할 정복을 시행한다면 한 원소를 생성하는 데 걸리는 시간 $O(1)$, 총 길이의 합 $O(NlogN)$이므로
총 시간 복잡도 $O(NlogN)$으로 구할 수 있게 됩니다.
테스트케이스 제작
C++의 <random> 헤더파일을 사용하여 구성하였습니다.
이때, Naive한 알고리즘이 통과되지 않도록 N과 M의 범위는 90000 이상으로 설정하였습니다.
tc_rand.cpp
#include "tc_rand.h"
void tc_rand()
{
random_device seed;
mt19937 gen(seed());
uniform_int_distribution<int> range(90000,100000);
uniform_int_distribution<int> range_n(1,300);
uniform_int_distribution<int> range_w(-10000,10000);
int n=range(seed);
printf("%d\n",n);
while(n--)
{
int w=range_w(seed);
printf("%d ", w);
}
n=range(seed);
printf("\n%d\n",n);
while(n--)
{
int w=range_w(seed);
printf("%d ", w);
}
}
string tc_filename(int tc_num, bool is_in) //테스트케이스 이름 문자열
{
string tc_name;
if(is_in) tc_name += "./in/test";
else tc_name += "./out/test";
string tcnum_str;
tcnum_str.resize(2);
tcnum_str[0]=tc_num/10+'0';
tcnum_str[1]=tc_num%10+'0';
tc_name += tcnum_str; //문자열 번호
if(is_in) tc_name += ".in";
else tc_name += ".out";
return tc_name;
}
void tc_make(int tc_num)
{
char tcname[201]={0}; //테케명
strcpy(tcname, tc_filename(tc_num, true).c_str());
FILE* fp=freopen(tcname,"w",stdout);
//조건에 맞는 테케 생성
tc_rand();
fclose(fp);
return;
}
답안 코드
위에서 설명한 고속 푸리에 변환을 구현해주면 됩니다.
해당 문제에서는 재귀함수를 활용하여 해결할 수 있도록 구성하였습니다.
#include <iostream>
#include <vector>
#include <string>
#include <complex>
#include <algorithm>
using namespace std;
typedef long double LF;
typedef long long int LL;
typedef complex<LF> cpx;
LF pi = acos(-1);
void FFT(vector<cpx> &v, cpx w)
{
int n = v.size();
if(n == 1) return;
vector<cpx> even(n/2), odd(n/2);
for(int i=0;i<n;i++)
{
if(i % 2 == 0) even[i/2] = v[i];
else odd[i/2] = v[i];
}
FFT(even, w*w);
FFT(odd, w*w);
cpx z(1,0);
for(int i=0;i<n/2;i++)
{
v[i] = even[i] + z * odd[i];
v[i + n/2] = even[i] - z * odd[i];
z *= w;
}
}
vector<LL> conv(vector<LL> a, vector<LL> b)
{
vector<LL> res(a.size() + b.size() - 1);
int n = 1;
while(n <= a.size() || n <= b.size()) n *= 2;
n *= 2;
a.resize(n);
b.resize(n);
vector<cpx> a_cpx(n), b_cpx(n);
for(int i=0;i<n;i++)
{
a_cpx[i] = cpx(a[i],0);
b_cpx[i] = cpx(b[i],0);
}
cpx w(cos(2 * pi / n), sin(2 * pi / n));
FFT(a_cpx, w);
FFT(b_cpx, w);
vector<cpx> res_cpx(n);
for(int i=0;i<n;i++) res_cpx[i] = a_cpx[i] * b_cpx[i];
FFT(res_cpx, cpx(1,0) / w);
for(int i=0;i<n;i++) res_cpx[i] /= cpx(n, 0);
for(int i=0;i<res.size();i++) res[i] = round(res_cpx[i].real());
return res;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
int n,m;
vector<LL> a,b;
cin >> n;
for(int i=0;i<n;i++)
{
int t;
cin >> t;
a.push_back(t);
}
cin >> m;
for(int i=0;i<m;i++)
{
int t;
cin >> t;
b.push_back(t);
}
vector<LL> res = conv(a,b);
for(int i=0;i<res.size();i++) cout << res[i] << ' ';
}
시행착오
시간제한을 별도로 설정하지 않았더니 TLE가 발생하였습니다.
FFT 자체가 꽤나 무거운 알고리즘이기 때문에, 문제의 시간 제한을 수정하였습니다.

느낀 점
지금까지 배워온 알고리즘 중 가장 어렵다고 생각한 알고리즘이였습니다.
그래도 계속해서 공부해보면서 이해하는 과정에서 성취감을 느꼈습니다.
또한, 자료를 더 조사해보니 비트 연산 등을 활용하여 비재귀로 FFT로 구성하면 최적화가 가능하다고 합니다.
이를 학습하여 최적화를 요구하는 문제를 제작해볼 생각입니다.
'과학고 조기졸업 과제 > AP 프로그래밍과 문제해결' 카테고리의 다른 글
| 4. RPG Extreme (0) | 2024.03.21 |
|---|---|
| 3. 주식회사 승범이네 (0) | 2024.03.15 |
| 2. 교수님은 기다리지 않는다 (1) | 2024.03.14 |
| 1. 잔디밭과 개미굴 (0) | 2024.03.14 |