1867번: 돌멩이 제거 (acmicpc.net)
solved.ac: Platinum III (2024.09.10)
a행 b열에 놓인 돌멩이를 제거하기 위해서는 a행을 쓸거나 b열을 쓸어야 한다.
그래프로 환원시키면, 1~n행과 1~m행 정점을 만들어 놓고,
간선을 돌로 정의해서, 해당 간선이 잇는 두 정점 중 하나가 색칠되면 된다라고 할 수 있다.
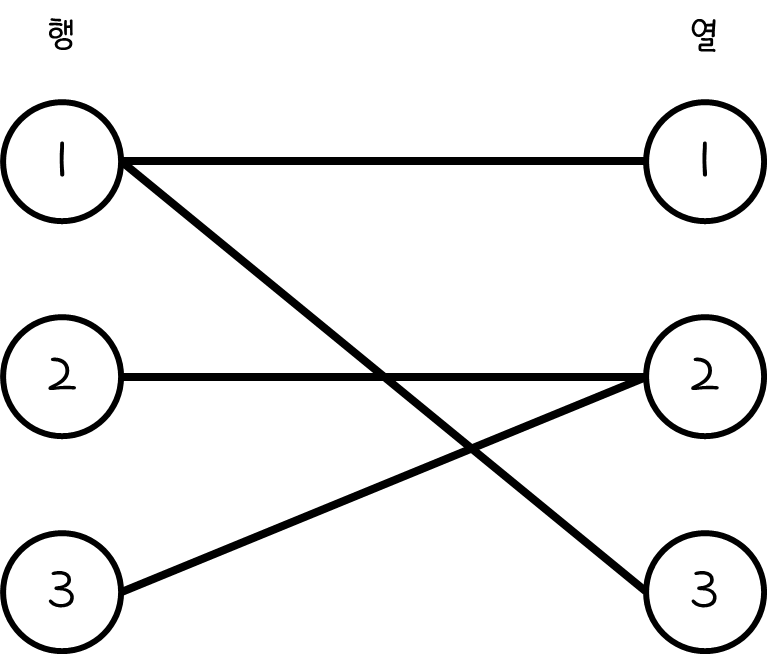
여기서는 1행을 쓸고, 2열을 쓸면 된다. 그래프로 나타내면, 다음과 같다.
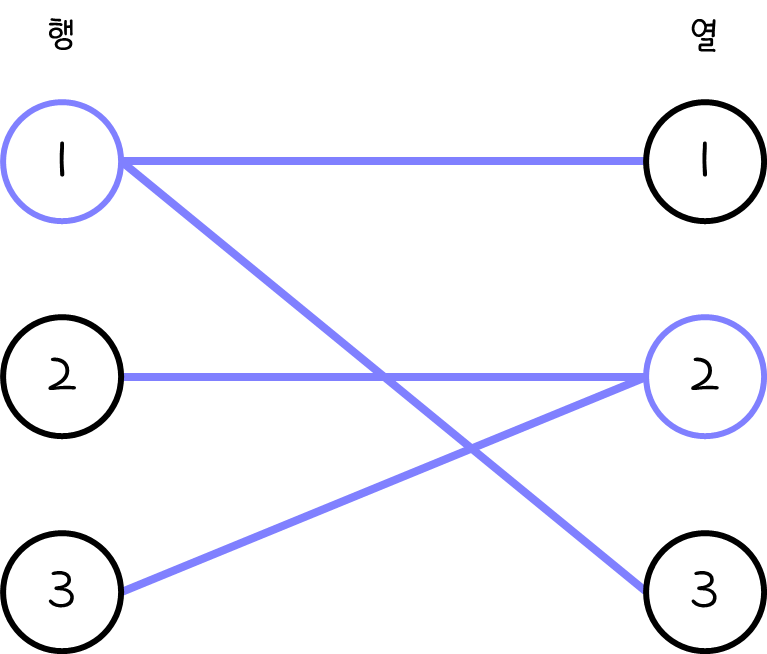
즉, 문제를 재정의하면 이분 그래프에서 최소한의 정점으로 모든 간선을 칠하는 방법을 찾는 문제가 된다.
이는 최소 정점 커버 문제 (Minimum Vertex Cover)로 알려져 있고, 이분 그래프의 경우 다항 시간 해법이 존재한다.
결론부터 말하면, 이분 그래프에서 최소 정점 커버의 해답은 이분 매칭의 최대 수와 동일하다.
이는 쾨닉의 정리(Konig's Theorem)로 잘 알려져 있다.
증명은 꽤나 어려워 보인다. 나중에 다시 공부해 봐야겠다.
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
/* 0 - based */
bool dfs(int cur, vector<vector<int>> &node, vector<int> &fromB, vector<bool> &vis)
{
for(auto nxt: node[cur])
{
if(vis[nxt]) continue;
vis[nxt] = true;
if(fromB[nxt] == -1 || dfs(fromB[nxt], node, fromB, vis))
{
fromB[nxt] = cur;
return true;
}
}
return false;
}
vector<pair<int, int>> BipartiteMatch(vector<vector<int>> &node)
{
int n = node.size();
vector<int> fromB(n, -1);
vector<bool> vis(n);
for(int i = 0; i < n; i++)
{
vis.assign(n, false);
dfs(i, node, fromB, vis);
}
vector<pair<int, int>> res;
for(int i = 0; i < n; i++) if(fromB[i] != -1) res.push_back({fromB[i], i});
sort(res.begin(), res.end());
return res;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
int n, k;
cin >> n >> k;
vector<vector<int>> node(2 * n);
for(int i = 0; i < k; i++)
{
int x, y;
cin >> x >> y;
x--; y--;
node[x].push_back(y + n);
}
cout << BipartiteMatch(node).size();
}
'Problem Solving' 카테고리의 다른 글
| BOJ 17501. 수식 트리 (0) | 2024.08.30 |
|---|---|
| BOJ 11378. 열혈강호 4 (0) | 2024.08.27 |
| BOJ 11012. Egg (0) | 2024.08.26 |
| BOJ 7626. 직사각형 (0) | 2024.08.26 |
| Aho-Corasick 알고리즘 (1) | 2024.08.26 |