solved.ac: Platinum II (2024.09.10)
각 직사각형별로 경계 또는 내부에 있는 점의 수를 세어 더하는 문제다.
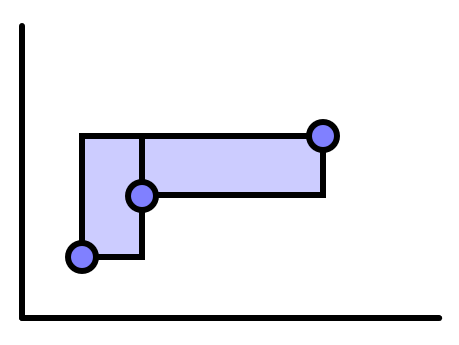
일단 직사각형을 하나씩 구해 보는 건 당연히 불가능할 것임을 짐작할 수 있다.
조금 생각을 바꿔서, 각 점별로 세지는 횟수를 구해 보자.
점별로 구하기 위해서는, 해당 점에 몇 개의 직사각형이 겹쳐 있는 지 파악해야 한다.
왼쪽부터 훑으면서 직사각형을 관리하는 것은 스위핑 기법이 잘 알려져 있다.
다음과 같이 직사각형의 시작과 끝을 구분해 보자. 푸른 색이 새로운 직사각형 시작, 빨간 색이 직사각형 끝이다.
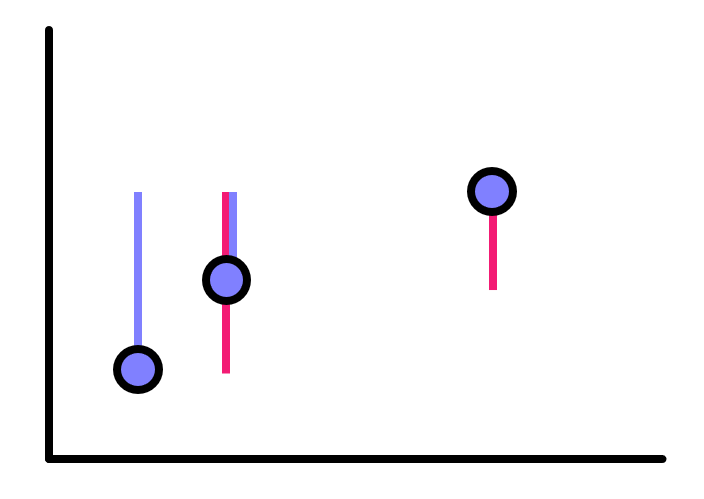
이제 왼쪽부터 스위핑을 하면서, 구간 업데이트를 통해 해당 위치에서의 직사각형 개수를 구하면 된다.
이는 lazyprop 세그트리를 이용하면 간단히 구할 수 있다.
마지막으로 두 번째 위치에서 쿼리 순서를 결정해야 하는 부분이 있다.
어떤 경계에서 직사각형이 끝난다 해도, 해당 위치에 점이 있다면 그 끝나는 직사각형에 걸치게 되므로
직사각형 종료 쿼리는 점 계산 쿼리보다 나중에 진행해야 한다.
즉, 동일한 x좌표의 쿼리에 우선순위를 매기면 다음과 같다.
- 새로운 직사각형 생성
- 점의 위치에 따른 직사각형 개수 계산
- 직사각형 종료
이제 구현만 하면 끝난다. 코드는 다음과 같다.
#include <iostream>
#include <vector>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long int LL;
LL tree[400001], lazy[400001];
void propagate(int node, int s, int e)
{
if(!lazy[node]) return;
tree[node] += (e - s + 1) * lazy[node];
if(s != e)
{
lazy[node * 2] += lazy[node];
lazy[node * 2 + 1] += lazy[node];
}
lazy[node] = 0;
}
LL update(int node, int s, int e, int l, int r, int val)
{
propagate(node, s, e);
if(r < s || e < l) return tree[node];
if(l <= s && e <= r)
{
tree[node] += val * (e - s + 1);
if(s != e)
{
lazy[node * 2] += val;
lazy[node * 2 + 1] += val;
}
return tree[node];
}
int m = (s + e) / 2;
LL left = update(node * 2, s, m, l, r, val);
LL right = update(node * 2 + 1, m + 1, e, l, r, val);
return tree[node] = left + right;
}
LL query(int node, int s, int e, int idx)
{
propagate(node, s, e);
if(idx < s || e < idx) return 0;
if(s == e) return tree[node];
int m = (s + e) / 2;
LL left = query(node * 2, s, m, idx);
LL right = query(node * 2 + 1, m + 1, e, idx);
return left + right;
}
void init()
{
memset(tree, 0, sizeof(tree));
memset(lazy, 0, sizeof(lazy));
}
struct Query
{
int op;
int x, y1, y2;
bool operator< (const Query &l)
{
if(x != l.x) return x < l.x;
return op > l.op;
}
};
void solve()
{
init();
int n, m;
cin >> n >> m;
vector<Query> arr;
while(n--)
{
int x, y;
cin >> x >> y;
arr.push_back({0, x, y, y});
}
while(m--)
{
int x1, x2, y1, y2;
cin >> x1 >> x2 >> y1 >> y2;
arr.push_back({1, x1, y1, y2});
arr.push_back({-1, x2, y1, y2});
}
sort(arr.begin(), arr.end());
LL res = 0;
for(auto i: arr)
{
int op = i.op;
int y1 = i.y1, y2 = i.y2;
if(op == 0) res += query(1, 0, 100000, y1);
else update(1, 0, 100000, y1, y2, op);
}
cout << res << '\n';
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
int T;
cin >> T;
while(T--) solve();
}
여담

그래서 이거 왜돼요
'Problem Solving' 카테고리의 다른 글
| BOJ 11378. 열혈강호 4 (0) | 2024.08.27 |
|---|---|
| BOJ 1867. 돌멩이 제거 (0) | 2024.08.27 |
| BOJ 7626. 직사각형 (0) | 2024.08.26 |
| Aho-Corasick 알고리즘 (1) | 2024.08.26 |
| BOJ 3665. 최종 순위 (0) | 2024.08.23 |