https://www.acmicpc.net/problem/3665
solved.ac: Gold I (2024.09.10)
약간의 애드혹 느낌이 있는 문제다.
문제에서 알아야 했던 것은, 상대적인 순위가 바뀐 모든 팀의 쌍을 주었다는 것이다.
즉 순위가 바뀌지 않은 팀도 모두 주었다는 것이다.
따라서 완전 그래프를 구성할 수 있고, 이를 위상 정렬하면 된다.
여담으로, 확실한 순위가 주어지지 않았으면 "?"을 출력하라는 것은 페이크다.
만약 확실한 순위가 주어지지 않았으면, 다음과 같이 두 정점 간의 우선순위 비교가 불가능한 경우이다.
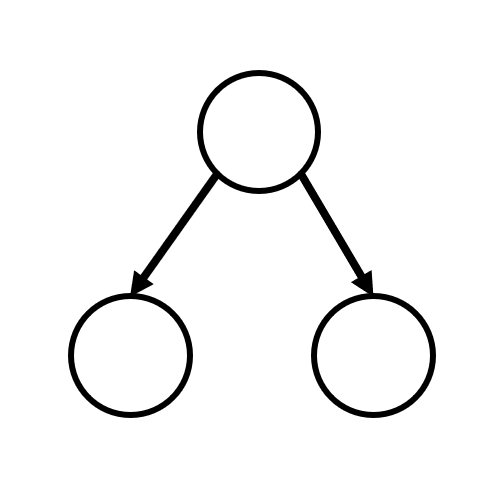
다시 정의하면, 방향 그래프에서 두 정점에 대해 한 정점에서 다른 정점으로 도달하는 것이 불가능하다는 것이다.
근데 애초에 완전 그래프이기 때문에, 이러한 경우는 불가능하다. 임의의 두 정점 사이에 간선이 있기 때문이다.
완전 그래프이므로 인접행렬도 딱히 상관은 없다. 인접행렬이 오히려 더 간편하기도 하다.
#include <iostream>
#include <vector>
#include <queue>
#include <cstring>
using namespace std;
int deg[501];
int node[501][501];
void init()
{
memset(deg, 0, sizeof(deg));
memset(node, 0, sizeof(node));
}
void solve()
{
init();
int n;
cin >> n;
vector<int> arr(n);
for(int i = 0; i < n; i++) cin >> arr[i];
for(int i = 0; i < n; i++)
{
for(int j = i + 1; j < n; j++)
{
node[arr[i]][arr[j]] = 1;
}
}
int m;
cin >> m;
while(m--)
{
int p, q;
cin >> p >> q;
if(node[p][q] == 0) swap(p, q);
node[p][q] = 0; node[q][p] = 1;
}
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= n; j++) deg[i] += node[j][i];
}
queue<int> q;
vector<int> res;
for(int i = 1; i <= n; i++)
{
if(deg[i] == 0) q.push(i);
}
while(res.size() < n)
{
if(q.empty())
{
cout << "IMPOSSIBLE";
return;
}
int cur = q.front();
q.pop(); res.push_back(cur);
for(int i = 1; i <= n; i++)
{
if(node[cur][i] == 1)
{
deg[i]--;
if(deg[i] == 0) q.push(i);
}
}
}
for(auto i: res) cout << i << ' ';
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
int T;
cin >> T;
while(T--)
{
solve();
cout << '\n';
}
}
'Problem Solving' 카테고리의 다른 글
| BOJ 7626. 직사각형 (0) | 2024.08.26 |
|---|---|
| Aho-Corasick 알고리즘 (1) | 2024.08.26 |
| BOJ 1450. 냅색문제 (0) | 2024.08.22 |
| BOJ 13896. Sky Tax (0) | 2024.08.13 |
| BOJ 2957. 이진 탐색 트리 (0) | 2024.08.12 |