solved.ac: Platinum III (2024.09.10)
문제를 요약하면, 루트 노드가 수시로 바뀌는 상황에서 서브트리 크기를 구하는 쿼리를 처리하라는 것이다.
일단 아직 뭐 rerooting technique라던가 배운 적도 없고, ETT는 쓸 생각도 못했다.
여기서는 쌩 LCA만 이용한 풀이를 작성한다.
처음 볼 때부터 그때그때 서브트리 크기를 직접 구하는 건 미친짓이라고 생각했다.
미리 한번 돌려서 크기를 구해놓고, 적절히 끼워맞추는 방식으로 접근했다.
이후 몇 개의 간단한 케이스워크를 통해 규칙을 찾았다.
이후의 모든 서술은 처음에 한번 잡고 돌린 트리를 기준으로 한다.
Case 1: 현재 루트노드가 쿼리 노드의 조상일 때
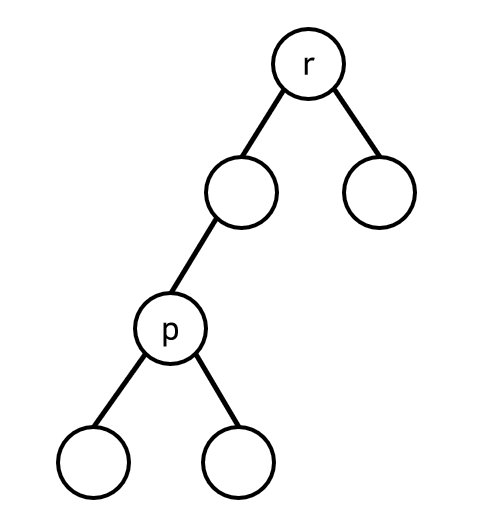
서브트리라는 것을 다시 생각해보면, p의 서브트리 내의 모든 정점들은 p의 조상으로 가기 위해서는 반드시 p를 거쳐야 한다.
따라서 r에서 쭉 내려가다가 p를 만나면, p에서 내려가는 모든 정점들은 항상 p를 거쳐가야 하게 된다. (트리의 부모는 항상 1개이므로)
이 경우 그냥 처음에 돌려놨던 서브트리 크기를 그대로 가져오면 된다.
Case 2: 쿼리 노드가 현재 루트노드의 조상일 때

r에서 p로 가는 경로가 유일하므로, 해당 경로를 거쳤다면 그 이후에 탐색하는 모든 정점들은 r에 도달하기 위해 반드시 p를 거쳐야 한다.
이는 서브트리 내의 노드의 성질과 일치한다.
조금 관점을 바꾸면 r에서 부모 노드를 타고 p로 갈 때, p의 직전 노드까지는 p를 거치지 않고도 r에 도달할 수 있음을 알 수 있다.
따라서 이 경우 p에서 r이 있는 방향으로 한 칸 내려가서, 이 정점을 s라 하면 n - sz[s]로 구할 수 있다.
한 칸 내려가는 경우가 조금 애매할 수 있다. 근데 돌이켜보면 희소 배열로 LCA 구할 때 마지막에 한 칸 올려주지 않았던가?
그 과정 생략하면 바로 얻을 수 있다. 아래 코드에선 따로 함수를 하나 더 짰다.
Case 3: LCA(cur, root) != cur, root
root에서 LCA로 가는 경로는 유일하고, cur과 LCA의 경우 Case 1과 겹친다. 따라서 그냥 서브트리 크기를 출력해주면 된다.
아래는 풀이 코드이다.
#include <iostream>
#include <vector>
#include <cstring>
using namespace std;
int n, root;
vector<int> node[100001];
int tree[100001];
int depth[100001];
int parent[100001][18];
int child[100001];
void init()
{
for(int i = 0; i < 100001; i++) node[i].clear();
memset(tree, 0, sizeof(tree));
memset(parent, 0, sizeof(parent));
}
int dfs(int cur, int prv = 0)
{
depth[cur] = depth[prv] + 1;
parent[cur][0] = prv;
tree[cur] = 1;
for(auto nxt: node[cur])
{
if(nxt == prv) continue;
tree[cur] += dfs(nxt, cur);
}
return tree[cur];
}
void structLCA()
{
for(int j= 1; j < 18; j++) for(int i = 1; i <= n; i++) parent[i][j] = parent[parent[i][j-1]][j-1];
}
int LCA(int p, int q)
{
if(depth[p] < depth[q]) swap(p, q);
int diff = depth[p] - depth[q];
for(int i = 0; i < 18; i++) if(diff & (1 << i)) p = parent[p][i];
if(p == q) return p;
for(int i = 17; i >= 0; i--)
{
if(parent[p][i] != parent[q][i])
{
p = parent[p][i];
q = parent[q][i];
}
}
return parent[p][0];
}
int LCAprv(int p, int q)
{
if(depth[p] < depth[q]) swap(p, q);
if(LCA(p, q) == q)
{
int diff = depth[p] - depth[q] - 1;
for(int i = 0; i < 18; i++) if(diff & (1 << i)) p = parent[p][i];
return p;
}
else
{for(int i = 17; i >= 0; i--)
{
if(parent[p][i] != parent[q][i])
{
p = parent[p][i];
q = parent[q][i];
}
}
return p;
}
}
void solve()
{
init();
int Q;
cin >> n >> Q >> root;
for(int i = 1; i < n; i++)
{
int p, q;
cin >> p >> q;
node[p].push_back(q);
node[q].push_back(p);
}
dfs(1); structLCA();
while(Q--)
{
int op, cur;
cin >> op >> cur;
if(op == 0) root = cur;
else
{
int prv = LCAprv(cur, root);
int lca = LCA(cur, root);
if(lca != cur) cout << tree[cur] << '\n';
else cout << n - tree[prv] << '\n';
}
}
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
int T;
cin >> T;
for(int i = 1; i <= T; i++)
{
cout << "Case #" << i << ":\n";
solve();
}
}'Problem Solving' 카테고리의 다른 글
| BOJ 3665. 최종 순위 (0) | 2024.08.23 |
|---|---|
| BOJ 1450. 냅색문제 (0) | 2024.08.22 |
| BOJ 2957. 이진 탐색 트리 (0) | 2024.08.12 |
| Centroid Decomposition (BOJ 5820) (0) | 2024.07.21 |
| 2024 KOI 1차 풀이 (0) | 2024.06.18 |