이번엔 트리 위에서 분할 정복을 해보려 합니다.
신난다
단순 배열 위에서 분할 정복을 했을 때를 생각해 봅시다.
대충 가운데를 잡고 반으로 쪼개면, 두 구간 모두 크기가 반이 되면서 두 개의 구간으로 나누어지므로
시간 복잡도 $O(NlogN)$이 보장됩니다.
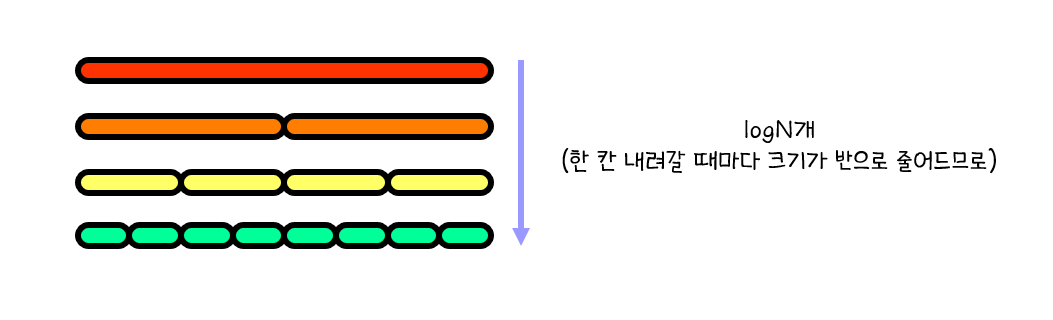
그렇다면 트리 위에서 분할 정복을 하려면 어떻게 해야 할까요?
트리에서 대충 배열에서의 가운데와 비슷한 역할을 하는 어떤 노드를 잡고 쪼개면,
나누어지는 서브트리 모두 크기가 반 이하가 되면 될 것 같이 생겼습니다.

여기서 센트로이드라는 개념이 등장합니다.
센트로이드(Centroid)는 지웠을 때 서브트리의 크기가 모두 원래 트리의 반 이하가 되도록 하는 노드를 의미합니다.
혹시 센트로이드가 없을 경우가 우려된다면, 다행히 모든 트리에는 센트로이드가 반드시 존재합니다.
만약 어떤 트리에서 센트로이드가 없다고 가정해 봅시다.
그렇다면 어떤 노드를 잡고 분해해도 크기가 전체의 반을 넘어가는 서브트리가 반드시 생겨난다는 뜻이 됩니다.
일단 반 이하로는 줄이지 못하더라도, 서브트리 크기 최댓값을 가장 작게 하는 노드 S를 하나 찾을 수 있을 것입니다.
그리고 그 큰 서브트리의 루트 노드 T를 잡으면, 대략적으로 다음과 같이 나타낼 수 있을 것입니다.
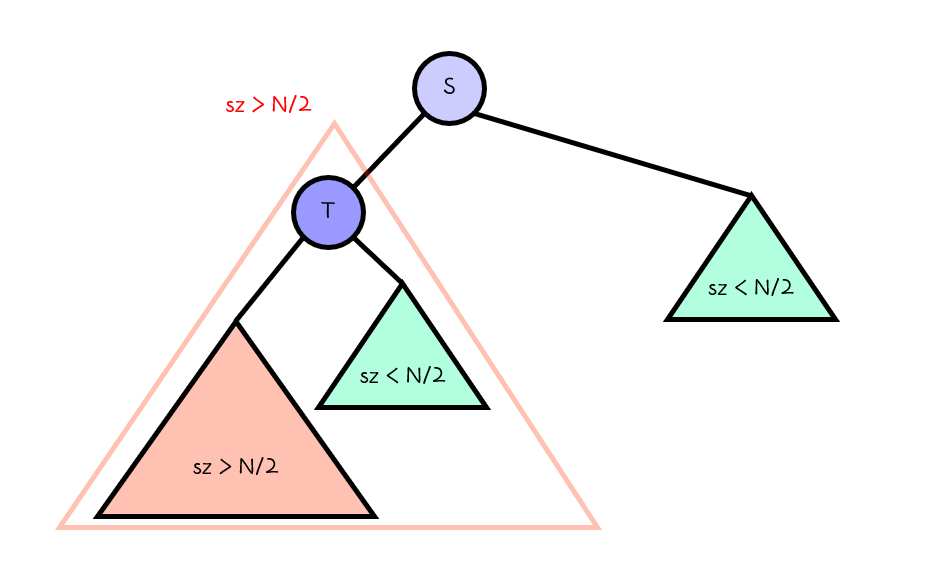
이때 T를 잡고 트리를 분해해도, 크기가 반 이하가 되면 안되므로 여전히 반 이상의 크기를 가지는 서브트리를 갖고 있어야 합니다.
근데 여기서 T를 잡고 트리를 분해해 본다면, S가 가지고 있던 서브트리보다 크기가 작아지므로
T로 분해한다면 서브트리의 크기의 최댓값이 S보단 작아질 것입니다.
아까 처음에 S를 잡고 분해했을 때 서브트리 크기 최댓값이 가장 작아진다고 했는데, 더 작아지는 정점 T를 찾았습니다.
즉 어디선가 가정 하나가 잘못되었다는 뜻이고, 지금 설정한 가정은 센트로이드가 없다는 것밖에 없습니다.
따라서 센트로이드가 없다는 가정이 잘못되었으므로 센트로이드는 항상 존재하게 됩니다.
(근데 이게 정확한 증명이 맞는지는 모르겠네요)
센트로이드를 구하는 알고리즘도 위와 비슷합니다.
이전과 달리 센트로이드가 항상 존재한다는 조건이 있으므로, 저 대충 큰 트리를 계속 타고 가다 보면
센트로이드를 발견할 수 있을 것이라 추측됩니다.
따라서, 한 정점을 잡고 크기를 구하기 위해 dfs를 돌린 후,
만약 서브트리 크기가 반 이상이 된다면 그 서브트리로 내려가 재귀적으로 탐색하여 센트로이드를 얻을 수 있습니다.
이때 서브트리의 루트노드 T를 다시 루트 노드로 잡는다 하면, 기존 서브트리의 부모 S를 루트로 하는 서브트리의 크기는
(전체 트리의 크기 - 기존의 T를 루트로 하는 서브트리의 크기)로 구할 수 있습니다.

코드로 나타내면 다음과 같습니다.
visited 배열의 의미는 현재 정점이 제거되었는지를 나타내기 위해 구성하였습니다.
int get_sz(int cur, int prv = -1)
{
sz[cur] = 1;
for(auto nxt: node[cur])
{
if(prv == nxt || visited[nxt]) continue;
sz[cur] += get_sz(nxt, prv);
}
return sz[cur];
}
int get_centroid(int cur, int prv, int tree_sz)
{
for(auto nxt: node[cur])
{
if(prv == nxt || visited[nxt]) continue;
if(sz[nxt] * 2 > tree_sz) return get_centroid(nxt, cur, tree_sz);
}
return cur;
}
이제 적절히 분할정복과 섞어서 문제를 해결해 주면 됩니다.
대표적인 예제 하나를 들고 와 보겠습니다.
https://www.acmicpc.net/problem/5820
요약하면 트리 위에서 길이가 K인 경로 중 간선의 개수를 최소로 하는 경로를 찾으라는 것입니다.
트리 위에서 임의의 두 정점을 잇는 경로는 반드시 하나라는 것을 상기하여, 다음과 같이 문제를 분할해볼 수 있습니다.
어떤 정점 S를 잡았을 때, 두 가지 경우를 확인해 주면 됩니다.
- S를 지나는 경로
- S를 지나지 않는 경로
S를 지나는 경로는 S로부터의 거리가 각각 L, K - L이면 해결될 것이고,
S를 지나지 않는 경로는 S를 제거함으로써 분할되는 서브트리 내에 경로가 존재하므로, 재귀적으로 탐색해 주면 됩니다.
이때 중요한 점은 S를 건너 두 경로를 연결할 때, 서로 다른 서브트리에서 S로 가는 경로여야 한다는 것입니다.
여기서 트리별로 한꺼번에 탐색하고, 한꺼번에 업데이트하는 방법으로 문제를 해결합시다.
먼저 min_depth[dist]에, 센트로이드를 기준으로 거리 dist만큼 떨어진 정점 중 거치는 간선의 개수의 최솟값을 저장합시다.
서브트리를 하나씩 순회하면서, min_depth 배열을 참조하여 서브트리를 하나씩 정복합시다.
예시로 아래와 같이 min_depth 배열을 업데이트한다고 생각하시면 됩니다.
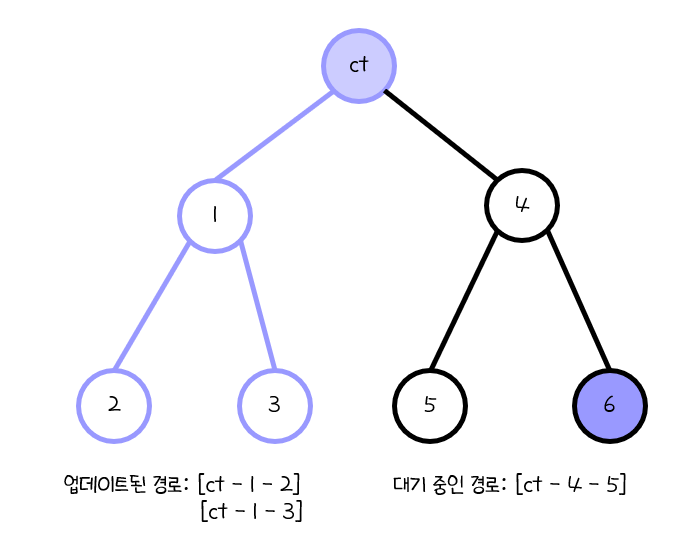
현재 센트로이드 ct를 잡고, 1, 2, 3, 4, 5를 탐색한 후 6번 정점을 탐색 중인 상황입니다.
ct - 4 - 5 경로는 아직 업데이트하지 않고, ct - 4 - 6 경로의 거리를 dist라 하면
min_depth[k - dist]를 참조하면 [ct - 1 - 2], [ct - 1 - 3] 경로에 의한 depth만을 참조할 수 있게 됩니다.
이러한 방식으로 경로를 연결하면 같은 서브트리 내에서 겹치는 경로가 존재하지 않으므로,
S를 지나는 경로만을 적절히 찾을 수 있습니다.
아래는 구현 코드입니다.
find_depth 함수는 dfs를 돌리면서 min_depth를 매칭시키는 함수,
update 함수는 서브트리 내 노드에 대해 min_depth를 업데이트하는 함수입니다.
이때 매번 100만개의 min_depth를 전부 초기화하는 건 비효율적이므로 업데이트된 dist만 따로 저장합시다.
int find_depth(int cur, int prv, int dist, int depth)
{
int res = INF;
if(dist > k) return INF;
res = min(res, depth + min_depth[k - dist]);
for(int i = 0; i < node[cur].size(); i++)
{
int nxt = node[cur][i];
int ndist = dist + cost[cur][i];
if(prv == nxt || visited[nxt]) continue;
res = min(res, find_depth(nxt, cur, ndist, depth + 1));
}
return res;
}
void update(int cur, int prv, int dist, int depth)
{
if(dist > k) return;
min_depth[dist] = min(min_depth[dist], depth);
updated_dist.push_back(dist);
for(int i = 0; i < node[cur].size(); i++)
{
int nxt = node[cur][i];
int ndist = dist + cost[cur][i];
if(prv == nxt || visited[nxt]) continue;
update(nxt, cur, ndist, depth + 1);
}
}
이제 지금까지 만든 함수들을 활용하여 분할 정복을 하면 문제를 해결할 수 있게 됩니다.
먼저 루트 하나를 잡고, 센트로이드를 찾습니다.
그 다음 센트로이드를 제거한 후, 서브트리별로 find_depth, update 함수를 순차적으로 번갈아가며 호출합니다.
모든 서브트리에 대해 호출이 끝났다면, 해당 트리에서 센트로이드를 지나는 경로는 모두 분석했습니다.
이후 각각의 서브트리에 대해 위의 과정을 반복하여 분할 정복을 하면 됩니다.
아래는 전체 코드입니다.
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
const int INF = 1e9;
int n, k;
int sz[200001];
bool visited[200001];
vector<int> node[200001], cost[200001];
int min_depth[1000001];
vector<int> updated_dist;
int get_sz(int cur, int prv = -1)
{
sz[cur] = 1;
for(auto nxt: node[cur])
{
if(prv == nxt || visited[nxt]) continue;
sz[cur] += get_sz(nxt, cur);
}
return sz[cur];
}
int get_centroid(int cur, int prv, int tree_sz)
{
for(auto nxt: node[cur])
{
if(prv == nxt || visited[nxt]) continue;
if(sz[nxt] * 2 > tree_sz) return get_centroid(nxt, cur, tree_sz);
}
return cur;
}
int find_depth(int cur, int prv, int dist, int depth)
{
int res = INF;
if(dist > k) return INF;
res = min(res, depth + min_depth[k - dist]);
for(int i = 0; i < node[cur].size(); i++)
{
int nxt = node[cur][i];
int ndist = dist + cost[cur][i];
if(prv == nxt || visited[nxt]) continue;
res = min(res, find_depth(nxt, cur, ndist, depth + 1));
}
return res;
}
void update(int cur, int prv, int dist, int depth)
{
if(dist > k) return;
min_depth[dist] = min(min_depth[dist], depth);
updated_dist.push_back(dist);
for(int i = 0; i < node[cur].size(); i++)
{
int nxt = node[cur][i];
int ndist = dist + cost[cur][i];
if(prv == nxt || visited[nxt]) continue;
update(nxt, cur, ndist, depth + 1);
}
}
int solve(int cur)
{
int tree_sz = get_sz(cur);
int centroid = get_centroid(cur, -1, tree_sz);
visited[centroid] = true;
int res = INF;
for(auto i: updated_dist) min_depth[i] = INF;
updated_dist.clear();
min_depth[0] = 0;
for(int i = 0; i < node[centroid].size(); i++)
{
int nxt = node[centroid][i];
int dist = cost[centroid][i];
if(visited[nxt]) continue;
res = min(res, find_depth(nxt, centroid, dist, 1));
update(nxt, centroid, dist, 1);
}
for(auto nxt: node[centroid])
{
if(visited[nxt]) continue;
res = min(res, solve(nxt));
}
return res;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cin >> n >> k;
for(int i = 0; i < n - 1; i++)
{
int p, q, dist;
cin >> p >> q >> dist;
node[p].push_back(q); cost[p].push_back(dist);
node[q].push_back(p); cost[q].push_back(dist);
}
for(int i = 0; i <= k; i++) min_depth[i] = INF;
int ans = solve(0);
cout << (ans == INF ? -1 : ans);
}
'Problem Solving' 카테고리의 다른 글
| BOJ 13896. Sky Tax (0) | 2024.08.13 |
|---|---|
| BOJ 2957. 이진 탐색 트리 (0) | 2024.08.12 |
| 2024 KOI 1차 풀이 (0) | 2024.06.18 |
| BOJ 2634. 버스노선 (1) | 2024.06.09 |
| BOJ 3295. 단방향 링크 네트워크 (0) | 2024.05.22 |