https://www.acmicpc.net/problem/2634
solved.ac: Platinum III (2024.09.10)
문제를 요약하면 다음과 같습니다.
- 리프 노드끼리 이어 경로를 구성한다. 이때 모든 간선은 정확히 한 번씩만 사용해야 한다.
예제의 경우를 예로 들면, 다음과 같이 구성하면 됩니다.
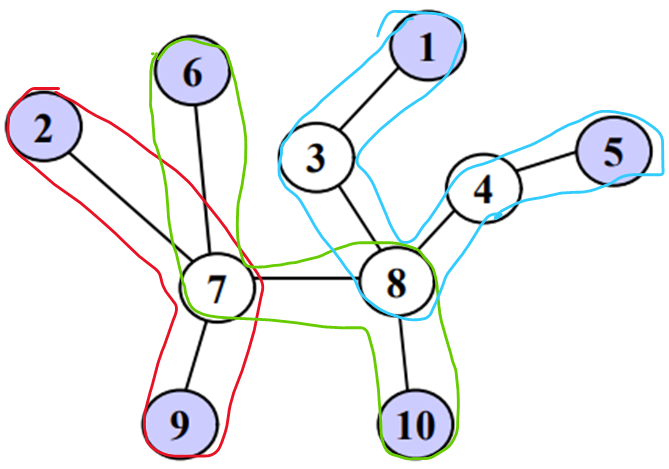
일단 트리라기엔 모양이 너무 예쁘지 않습니다. 한번 다음과 같이 다시 그려 봅시다.
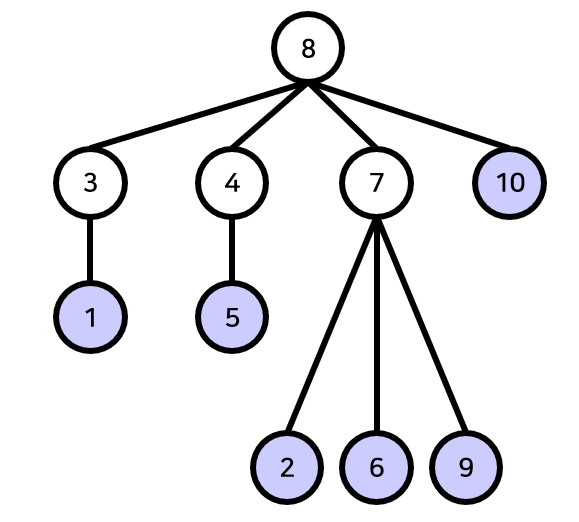
먼저 리프 노드가 아닌 경우, 해당 그림에서는 색칠되지 않은 그림의 경우 항상 노드의 차수가 짝수가 되어야 합니다.
이유는 문제에서 리프 노드끼리만 경로를 이어야 하기 때문입니다.
만약 해당 노드가 어떠한 경로에 포함된다면, 리프 노드가 아니므로 반드시 해당 간선은 어떠한 경로 중간에 있게 됩니다.
따라서 항상 두 개의 간선이 잇게 되므로, 절대로 홀수 개가 될 수 없습니다.
또한 이를 비틀어서, 리프 노드를 제외한 모든 정점의 차수가 짝수라면 항상 경로가 존재할까요?
이 역시 마찬가지로 성립합니다.
먼저 그래프의 모든 정점의 차수를 더하면 짝수가 되므로, 리프 노드가 홀수개는 될 수 없습니다.
그렇다면 분명 간선이 모자라거나 남는 경우일 것입니다.
어떠한 경로를 구성했을 때 간선 일부가 겹친다고 생각하면, 다음과 같이 일반화할 수 있습니다.
경로 1: A → E → F → B
경로 2: C → E → F → D
이 경우 두 경로를 각각
A → E → C
B → F → D
로 바꾸어 주면, 겹치는 부분을 없앨 수 있습니다.
간선 일부가 사용되지 않았을 경우, 그 간선을 제거하여도 경로는 문제가 없습니다.
이때 모든 정점의 차수가 홀수 개여야 하므로 하나의 간선이 더 제거될 것입니다.
이를 반복적으로 수행하면, 결국 리프 노드를 잇는 간선이 제거되므로 모순이 발생합니다.
따라서 위의 조건을 통해 반드시 존재할 것이다 / 반드시 불가능하다 를 판별할 수 있습니다.
이제 경로를 구성합시다.
여기서는 그냥 가장 경로가 짧은 것을 위로 보내는 그리디를 활용했습니다.
테스트케이스가 약한 감이 없지않아 있긴 합니다. 딱히 될 것 같은 그리디는 아닌데 풀리네요.
풀면서도 조금 의아했던 점은 정점 하나만 들고 왔을 때는 틀렸는데,
모든 정점을 다 루트 노드로 놓고 돌리면 또 풀립니다. 왜 이러지
#include <iostream>
#include <vector>
#include <algorithm>
#include <queue>
#include <cstring>
using namespace std;
vector<int> node[501];
int n;
bool leaf[501], used[501];
int depth[501], link[501];
int parent[501];
bool cmp(int i, int j){return depth[i] < depth[j];}
int dfs(int cur, int prv)
{
depth[cur] = depth[prv] + 1;
if(leaf[cur]) return cur;
vector<int> arr;
for(auto nxt: node[cur])
{
if(nxt == prv) continue;
arr.push_back(dfs(nxt, cur));
}
sort(arr.begin(), arr.end(), cmp);
int s = arr.size() % 2, e = arr.size() - 1;
while(s < e)
{
link[arr[s]] = arr[e];
link[arr[e]] = arr[s];
used[arr[s]] = true;
used[arr[e]] = true;
s++; e--;
}
return arr[0];
}
void find(int cur, int prv)
{
parent[cur] = prv;
for(auto nxt: node[cur])
{
if(nxt == prv) continue;
find(nxt, cur);
}
}
int len = 10005;
vector<vector<int>> ans;
void solve()
{
int mx = -1;
vector<vector<int>> res;
for(int i=1;i<=n;i++)
{
if(used[i] == false) continue;
memset(parent, 0, sizeof(parent));
int p = i, q = link[i];
used[p] = false; used[q] = false;
find(p, 0);
vector<int> route;
while(q != p)
{
route.push_back(q);
q = parent[q];
}
route.push_back(p);
res.push_back(route);
mx = max(mx, (int)route.size() - 1);
}
if(mx < len)
{
len = mx;
ans = res;
}
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cin >> n;
for(int i=1;i<n;i++)
{
int p,q;
cin >> p >> q;
node[p].push_back(q);
node[q].push_back(p);
}
//가능한지 판별
for(int i=1;i<=n;i++)
{
if(node[i].size() > 1 && node[i].size() % 2 == 1)
{
cout << 0;
return 0;
}
if(node[i].size() == 1) leaf[i] = true;
}
//탐색
for(int i=1;i<=n;i++)
{
if(leaf[i]) continue;
memset(used, 0, sizeof(used));
memset(depth, 0, sizeof(depth));
memset(link, 0, sizeof(link));
memset(parent, 0, sizeof(parent));
depth[0] = -1;
dfs(i, 0);
solve();
}
cout << len << '\n';
cout << ans.size() << '\n';
for(int i=0;i<ans.size();i++)
{
for(auto j: ans[i]) cout << j << ' ';
cout << '\n';
}
}
'Problem Solving' 카테고리의 다른 글
| Centroid Decomposition (BOJ 5820) (0) | 2024.07.21 |
|---|---|
| 2024 KOI 1차 풀이 (0) | 2024.06.18 |
| BOJ 3295. 단방향 링크 네트워크 (0) | 2024.05.22 |
| Heavy-Light Decomposition (1) | 2024.05.21 |
| BOJ 28327. 지그재그 (0) | 2024.05.20 |