solved.ac: Platinum I (2024.09.06)
KOI 2023 본선 2번으로 출제된 문제입니다.
https://www.acmicpc.net/problem/28327
문제를 요약하면,
- 길이 $N$의 1부터 $N$까지의 자연수를 모두 원소로 가지는 수열이 주어진다.
- 각각의 수 $x$에 대하여, 서로 다른 모든 구간에 대하여 지그재그 수열의 최대 길이의 합을 구하여라.
이 되겠습니다.
$O(N^{3})$ 풀이
개인적으로 이 문제를 보자마자 $O(N^{2})$를 짜는 건 사실상 천재의 영역이라 생각됩니다.
따라서, 핵심 아이디어를 뽑아내고 이를 먼저 나이브하게 구현해 보겠습니다.
지그재그 수열을 더 길게 만들고 싶다면, 바로 앞의 두 수와 이번에 추가할 수에 대하여
계속 증가하거나 계속 감소하는, 단조성을 띄지만 않으면 된다는 것을 알 수 있습니다.
당장 바로 앞의 것만 보면 된다는 점에서, 그리디가 성립하지 않을까 라는 추측을 해볼 수 있습니다.
그리고 실제로 성립합니다.
간단한 테스트케이스로, [1, 2, 4, 3] 을 생각해 봅시다.
대충 앞에서부터 1, 2를 먼저 놓으면, 정의에 의해 일단 길이 2의 지그재그 수열을 만들 수 있습니다.
그리고 4를 이어붙이려는데, 1 < 2 < 4라서 4를 이어붙일 수는 없습니다.
여기서 가능한 행동은 2가지가 존재합니다.
- 만들고 있는 지그재그 수열을 [1, 2]로 유지한다.
- 2를 지우고, 4를 추가함으로써 지그재그 수열을 [1, 4]로 유지한다.
전자의 경우 3 역시 이어붙일 수가 없는 반면,
후자의 경우 [1, 4, 3]으로 길이 3의 지그재그 수열을 만들 수 있습니다.
현재 만들어진 지그재그 수열의 맨 뒤의 두 항을 $a, b$라 하고, 현재 이어붙일 수와 다음에 이어붙일 수를 $c, d$라 합시다.
만약 계속 지그재그가 성립한다면 계속 이어붙이면 되므로, $a, b, c$ 순으로 나열할 때 단조적인 경우만 생각해 봅시다.
$a, b, c, d$를 나열했을 때, 단조성을 띠는 경우는 다음 두 가지가 존재합니다.
- $a, b, c, d$
- $a, b, d, c$
전자의 경우 $c, d$를 사용해도 길이를 늘릴 수는 없습니다.
그러나 후자의 경우 $a, c, d$ 꼴로 구성한다면 지그재그 수열의 길이를 늘릴 수 있습니다.
이때 전자의 경우에도 $a, c$로 바꿀 수는 있다는 점에서, 일단 단조성을 띠는 경우 무조건 바꾸는 것이 이득임을 알 수 있습니다.
따라서, 단조성을 띤다면 바꾸고, 그렇지 않다면 이어붙임으로써 길이를 최대한으로 늘릴 수 있습니다.
이를 활용하여 다음 풀이를 이용하여 서브테스크 3까지 통과할 수 있습니다.
#include <iostream>
#include <vector>
using namespace std;
int arr[200001];
int g[200001];
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
int n;
cin >> n;
for(int i=1;i<=n;i++) cin >> arr[i];
for(int x=1;x<=n;x++)
{
for(int y=1;y<=n;y++)
{
vector<int> v;
int dir = 0;
for(int z=y;z<=n;z++)
{
int cur = arr[z];
if(cur <= x)
{
if(v.size() < 2)
{
v.push_back(cur);
if(v.size() == 2) dir = v[0] > v[1] ? 1 : -1;
}
else
{
int nxt_dir = v.back() > cur ? 1 : -1;
if(dir != nxt_dir)
{
v.push_back(cur);
dir = nxt_dir;
}
else v[v.size() - 1] = cur;
}
}
g[x] += v.size();
}
}
}
for(int i=1;i<=n;i++) cout << g[i] << '\n';
}$O(N^{2})$ 풀이
수열의 길이는 곧 수열의 원소의 개수와 같습니다.
따라서, 각 원소가 등장하는 횟수를 더해 준다면 $g$의 값을 구할 수 있습니다.
이전의 그리디 풀이에서, 단조성을 띠지 않는다면 해당 수는 무조건 사용됨을 알 수 있습니다.
이를 활용하여, 조금 더 수학적으로 문제를 해결해 봅시다.
일단 어떤 수가 항상 사용된다고 가정한다면, 해당 수를 포함하는 부분수열의 개수는 다음과 같이 나타낼 수 있습니다.
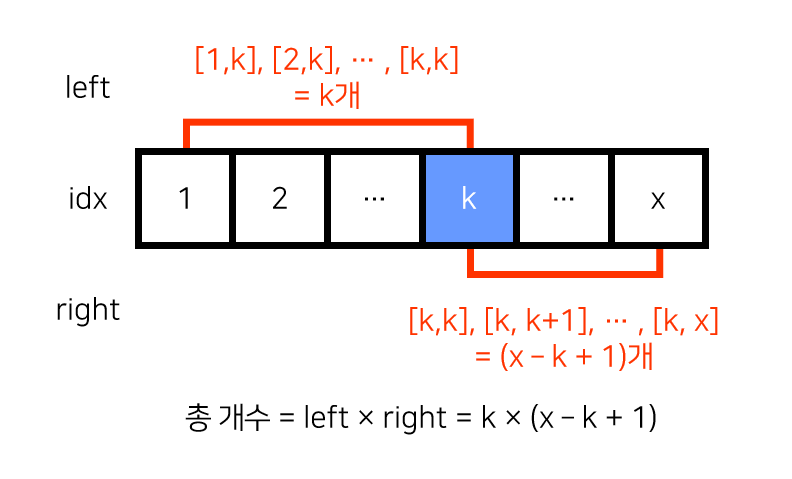
이제 어떤 k번째 수가 사용되지 않는 부분수열의 개수를 구해 봅시다.
우선 어떤 수가 맨 마지막에 위치한다면, 그리디 풀이에서 이 수는 무조건 사용됨을 알 수 있습니다.
또한, 만약 k-1번째 수, k번째 수, k+1번째 수가 단조성을 띤다면, k+1번째 수가 사용되고 나서부터는 사용되지 않음을 알 수 있습니다.
따라서 단조성을 띠는 경우, right 중 가능한 경우는 자기 자신만 포함하는 경우밖에 없게 됩니다.
이 경우 어떤 수가 포함되는 부분 배열의 개수는 k개만 존재합니다.
이를 그대로 구현해 준다면 서브테스크 4를 해결할 수 있습니다.
#include <iostream>
#include <vector>
using namespace std;
typedef long long int LL;
int arr[200001];
LL idx[200001];
LL g[200001];
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
LL n;
cin >> n;
for(int i=1;i<=n;i++)
{
cin >> arr[i];
idx[arr[i]] = i;
}
for(int x=1;x<=n;x++)
{
vector<int> v;
for(LL k=1;k<=n;k++)
{
if(arr[k] <= x) v.push_back(arr[k]);
}
LL sz = v.size();
for(LL i=0;i<sz;i++) g[x] += idx[v[i]] * (n + 1 - idx[v[i]]);
for(LL i=1;i<sz-1;i++)
{
if( (v[i-1] > v[i] && v[i] > v[i+1]) || (v[i-1] < v[i] && v[i] < v[i+1]) )
{
g[x] -= idx[v[i-1]] * (n + 1 - idx[v[i+1]]);
}
}
}
for(int i=1;i<=n;i++) cout << g[i] << '\n';
}$O(NlogN)$ 풀이
1부터 x까지 있는 부분 배열에서 x+1이 추가될 때, 단조성이 바뀔 수 있는 경우의 수는 x+1 양 옆에 존재하는 수들입니다.
따라서 업데이트를 하며 좌우의 경우에만 배열의 수를 수정해 준다면 문제를 해결할 수 있습니다.
공식 풀이나 제 풀이 같은 경우 <set>을 사용하였고, k번째 수를 관리해준다는 점에서 세그먼트 트리를 활용할 수도 있습니다.
#include <iostream>
#include <set>
using namespace std;
typedef long long int LL;
LL n, res;
LL idx[200001];
LL a[200001];
set<int> v; //인덱스
int prv(int cur)
{
if(v.find(cur) == v.begin() || cur == 0) return 0;
return *--v.find(cur);
}
int nxt(int cur)
{
if(v.find(cur) == --v.end() || cur == 0) return 0;
return *++v.find(cur);
}
bool is_monotone(int i, int j, int k)
{
if(a[i] > a[j] && a[j] > a[k]) return true;
if(a[i] < a[j] && a[j] < a[k]) return true;
return false;
}
void add(int cur)
{
res += cur * (n + 1 - cur);
int p1 = prv(cur), n1 = nxt(cur);
if(p1 * n1 && is_monotone(p1, cur, n1)) res -= p1 * (n + 1 - n1);
}
void undo(int cur)
{
int p2 = prv(prv(cur)), p1 = prv(cur);
int n1 = nxt(cur), n2 = nxt(nxt(cur));
if(p2 * n1) if(is_monotone(p2, p1, n1)) res += p2 * (n + 1 - n1);
if(p2) if(is_monotone(p2, p1, cur)) res -= p2 * (n + 1 - cur);
if(p1 * n2) if(is_monotone(p1, n1, n2)) res += p1 * (n + 1 - n2);
if(n2) if(is_monotone(cur, n1, n2)) res -= cur * (n + 1 - n2);
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cin >> n;
for(int i=1;i<=n;i++)
{
cin >> a[i];
idx[a[i]] = i;
}
for(int i=1;i<=n;i++)
{
v.insert(idx[i]);
add(idx[i]); undo(idx[i]);
cout << res << '\n';
}
}
'Problem Solving' 카테고리의 다른 글
| BOJ 2634. 버스노선 (1) | 2024.06.09 |
|---|---|
| BOJ 3295. 단방향 링크 네트워크 (0) | 2024.05.22 |
| Heavy-Light Decomposition (1) | 2024.05.21 |
| 함수 개형을 이용한 최적화 (Slope Trick) (0) | 2024.05.17 |
| 히르쉬버그 (Hirschberg) 알고리즘 (0) | 2024.04.03 |