일단 시간복잡도는 제껴두고, 이 문제를 풀어봅시다.
13323번: BOJ 수열 1 (acmicpc.net)
만약 $N \le 10000$ 정도라면, 약간의 관찰을 통한 간단한 $O(N^{2})$ DP를 통해 해결할 수 있습니다.
대충 '$DP(x, k) = x$번째 값을 $k$로 만들었을때 최소 연산 어쩌구' 꼴로 구성해주고,
$DP(x, k) = \min (1 \le i \le k - 1) DP(x-1, i) + |a[x] - k| $ 이라 정의하여 간단히 해결할 수 있습니다.
하지만 만약 $N$이 무지막지하게 커져서, 한 $10^{6}$ 쯤 된다고 해봅시다.
그러면 당연히 시간 내에 풀 수 없을 것입니다. 물론 그 전에 메모리가 터지겠지만요.
문제를 해결하기 위해서는 DP(x, k)를 k에 따른 함수로 해석하는 아이디어가 필요합니다.
먼저 x = 1일 때만 생각해보면, $DP(0, k) = 0$이므로, $DP(1, k) = |a[1] - k|$ 이라 할 수 있습니다.
대충 그래프로 나타내면 이렇게 될 것입니다.

그런데 만약 DP(2, k)를 구할 때, $ k \ge a_{1}$이라면 더 최소화할 수 있음에도 불구하고,
굳이 더 크게 만들 이유는 전혀 없습니다. 따라서 그래프를 다음과 같이 바꾸어 볼 수 있습니다.
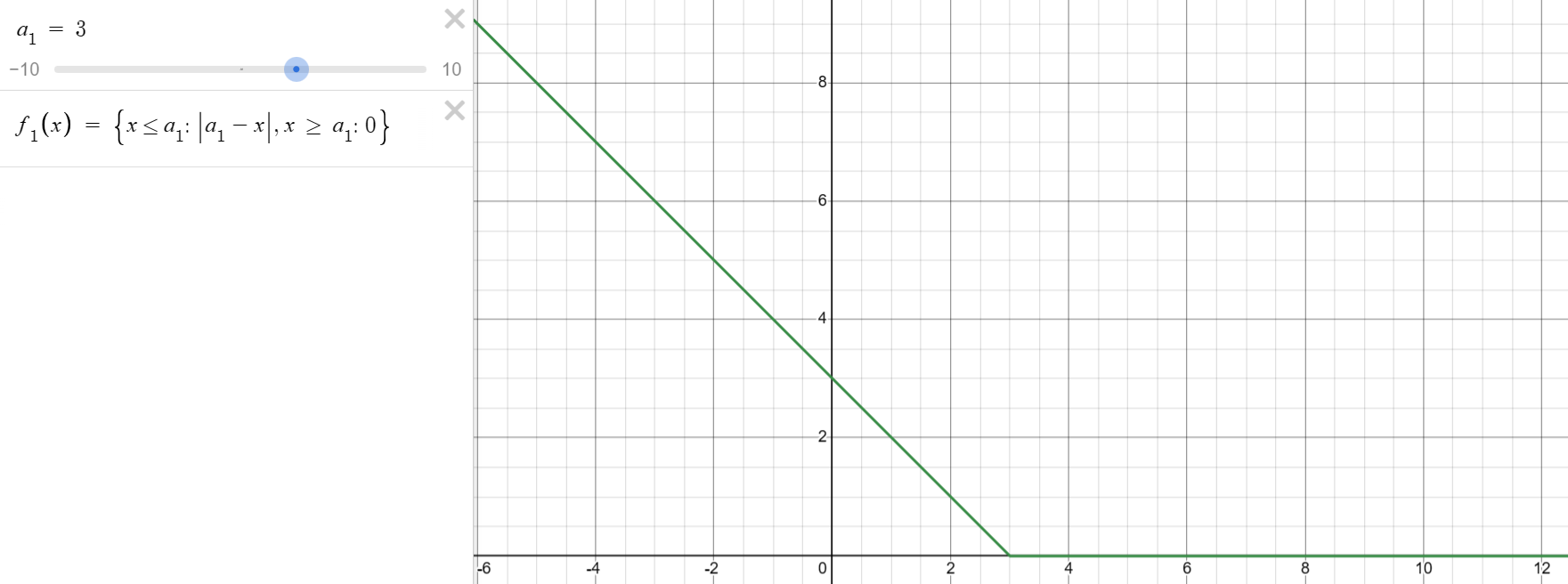
이제 DP(2, k)를 구해 봅시다.
먼저 이전의 작업을 통해 DP 함수에서 증가하는 부분이 없게끔 미리 만들어 놓았습니다.
따라서 k 이하의 모든 수를 고려할 필요 없이, 그냥 $DP(2, k) = DP(1, k) + |a_{2} - k|$으로 식을 구성하여도 충분합니다.

이제 $DP(3, k), DP(4, k)$ 등 계속해서 같은 원리를 적용하기 위해서, 증가하는 부분을 다시 평평하게 만들어 주어야 합니다.
이 때부터는 2가지의 경우가 나타나게 되고, 이를 고려해 주어야 합니다.
여기서부터는 이후의 설명을 위해, 기울기의 관점에서도 확인할 것입니다.
i) $a_{1} > a_{2}$

이 경우 평평해지는 부분의 높이는 $a_{1} - a_{2}$만큼 증가하게 됩니다.
이때 점 $a_{2}$를 기준으로 기울기는 2만큼 변하게 됩니다.
ii) $a_{1} \le a_{2}$
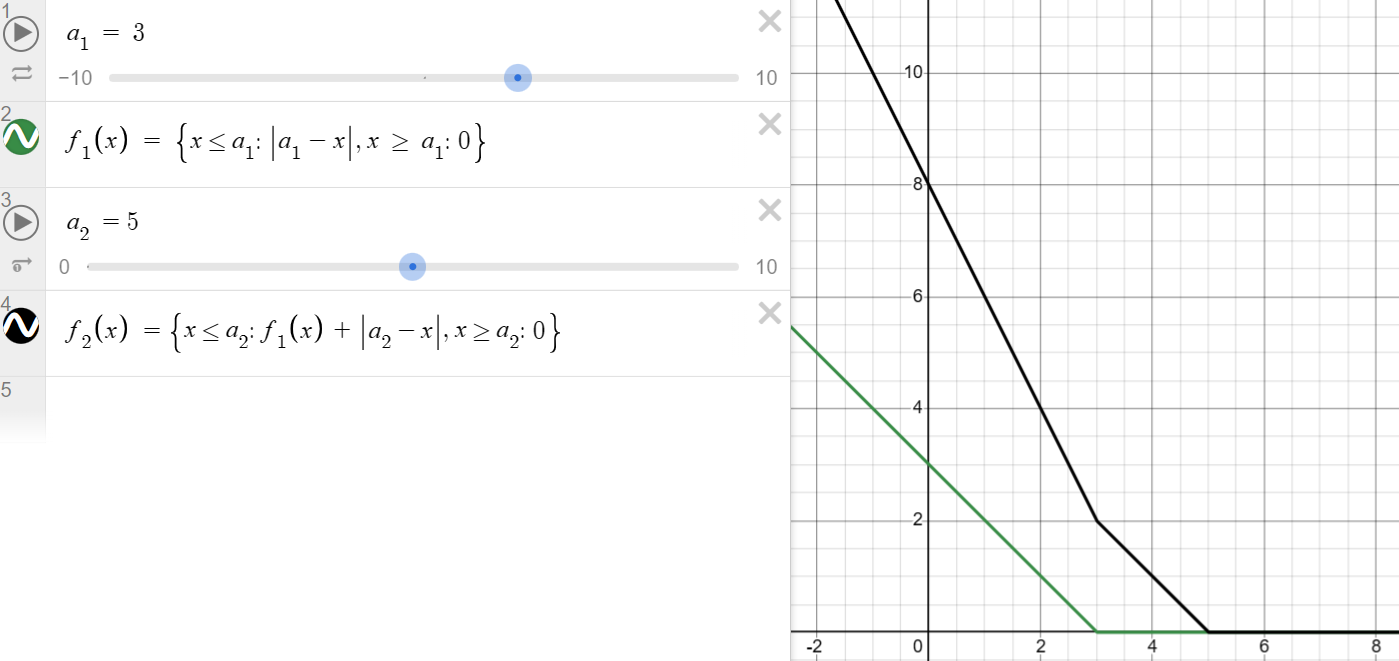
이 경우 처음으로 평평해지는 부분의 높이는 변하지 않았습니다.
이때 점 $a_{2}$를 기준으로, 기울기는 1만큼 변하게 됩니다.
딱히 아직까진 마땅한 규칙이 보이지 않습니다.
일단 마찬가지로 평탄해진 부분에 대해 그 이후는 쭉 밀어버리고, $DP(3, k)$까지 한번 구해 봅시다.


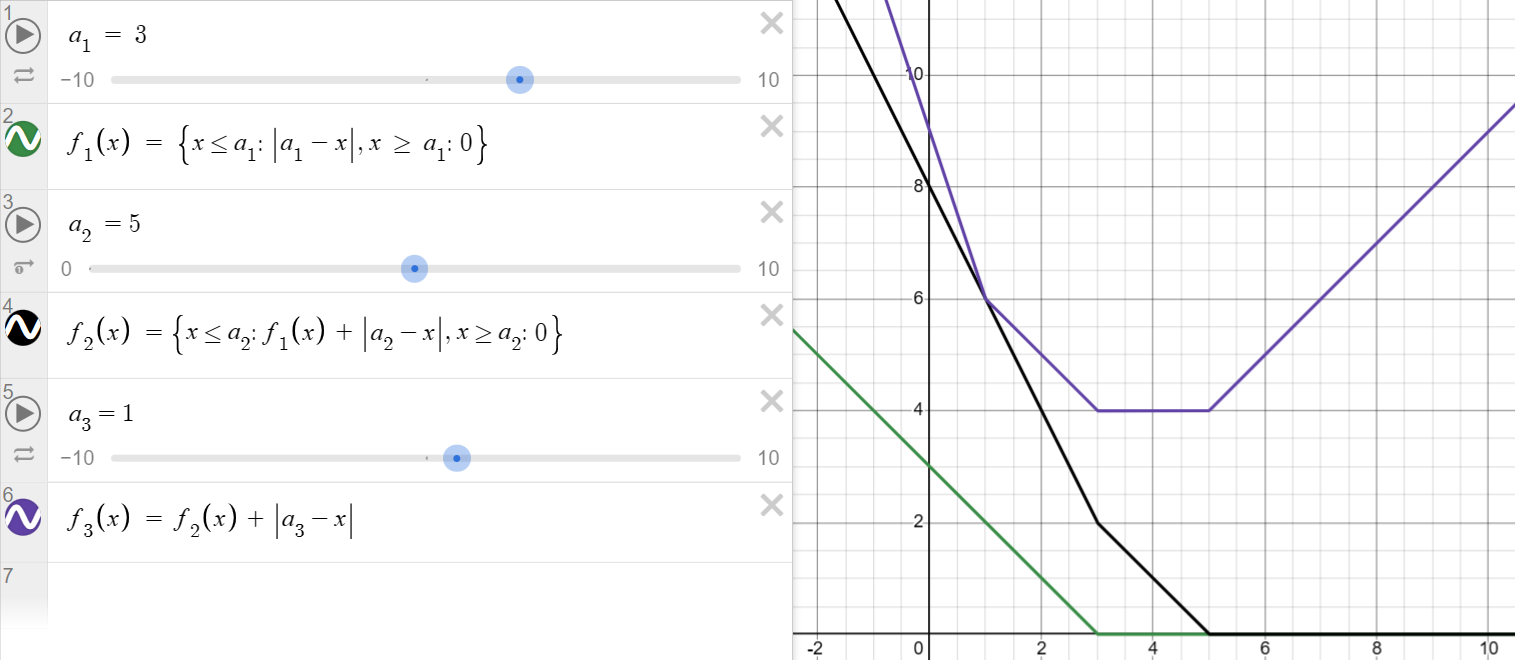
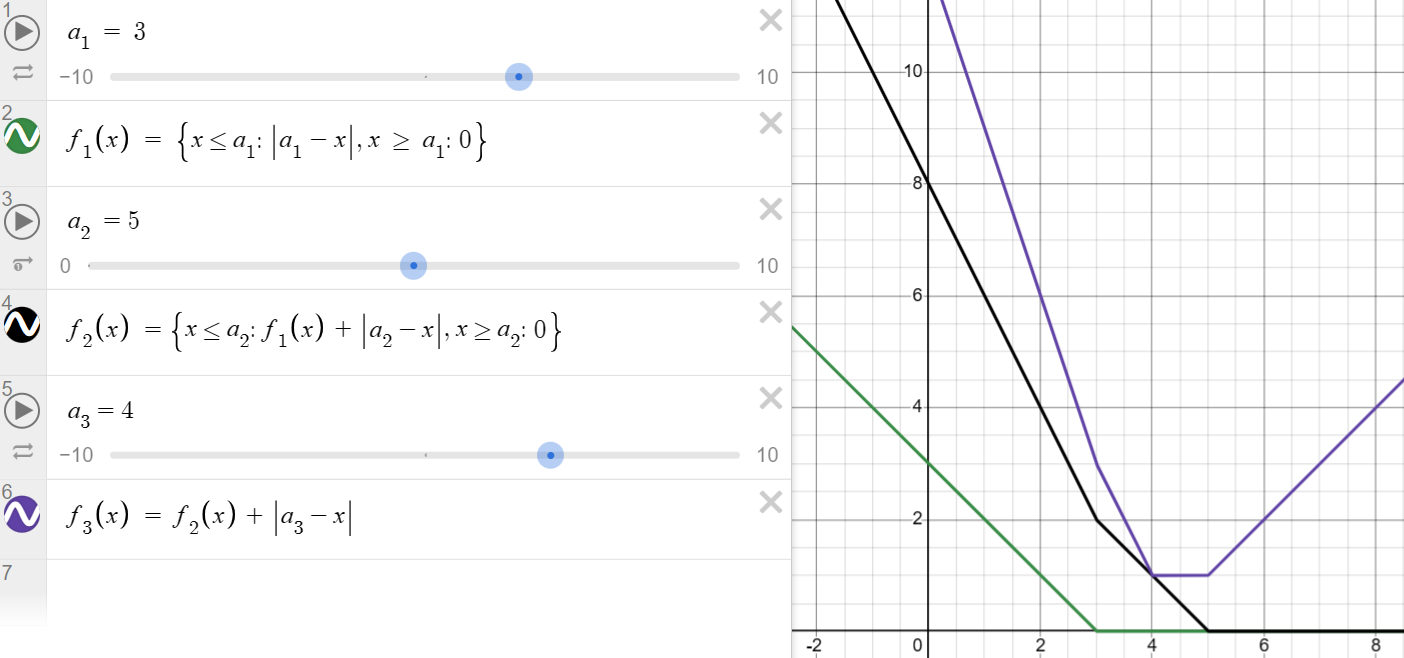
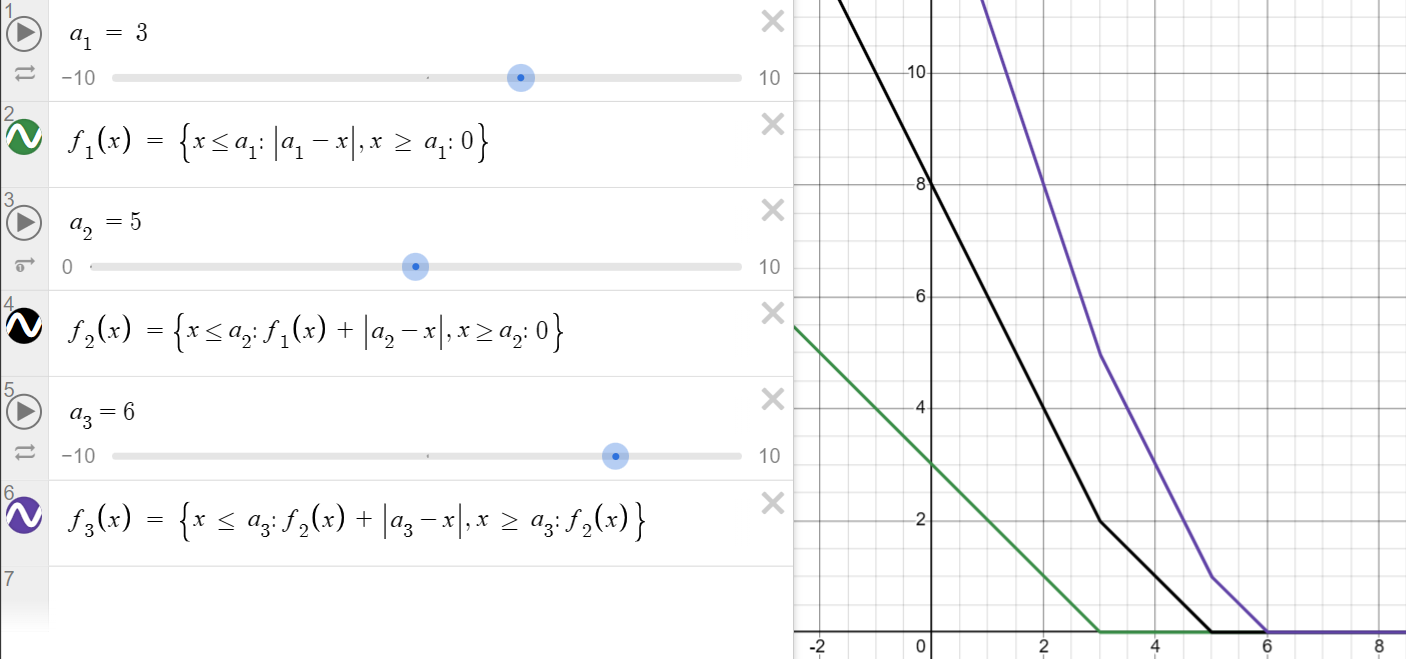
(이전의 그래프에서 평탄해지는 지점)을 중점적으로 관찰해봅시다.
먼저 현재 지점이 (이전의 그래프에서 평탄해지는 지점)보다 왼쪽에 위치하는 경우입니다.
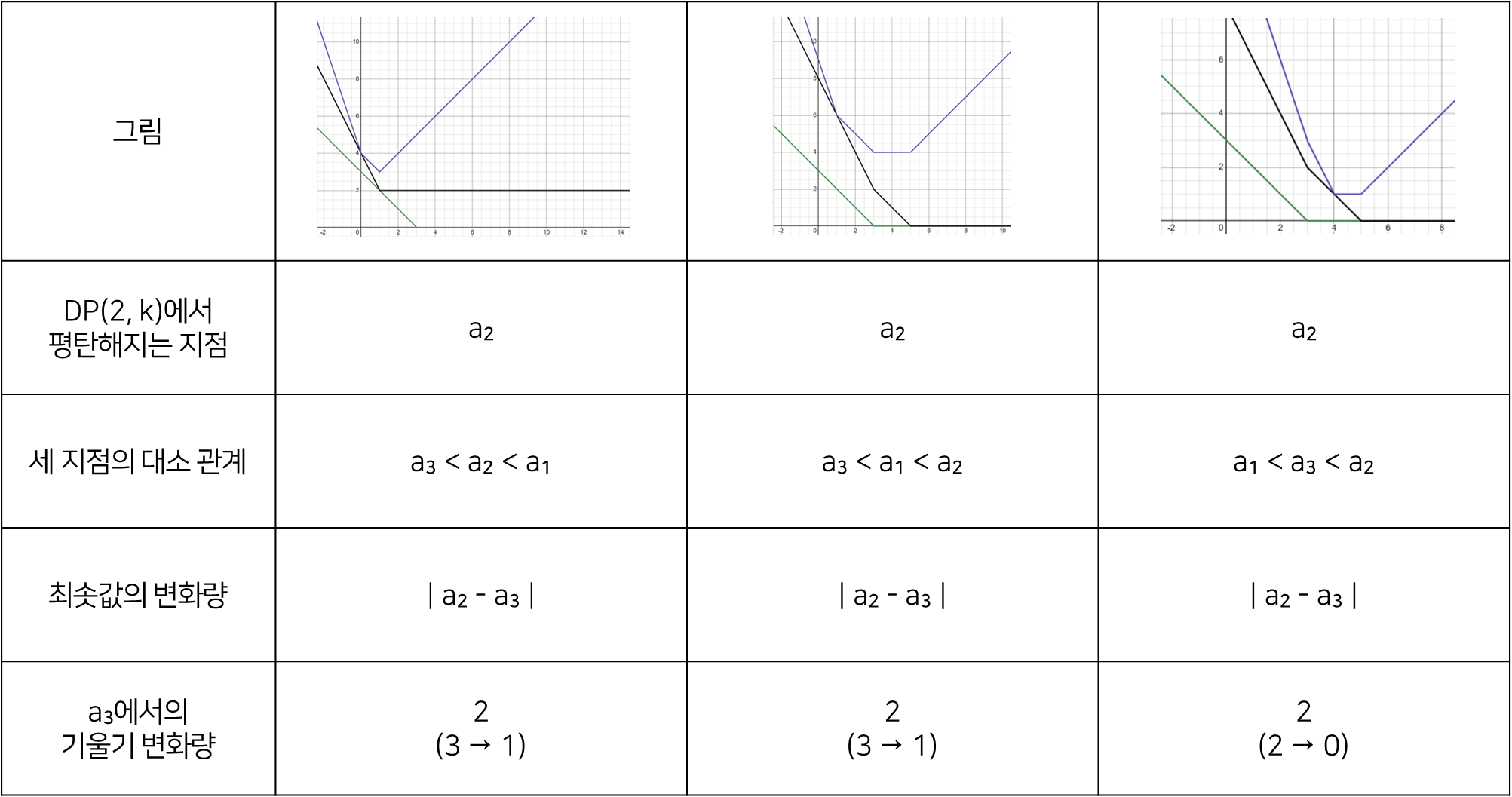
다음은 현재 지점이 (이전의 그래프에서 평탄해지는 지점)보다 오른쪽에 위치하는 경우입니다.
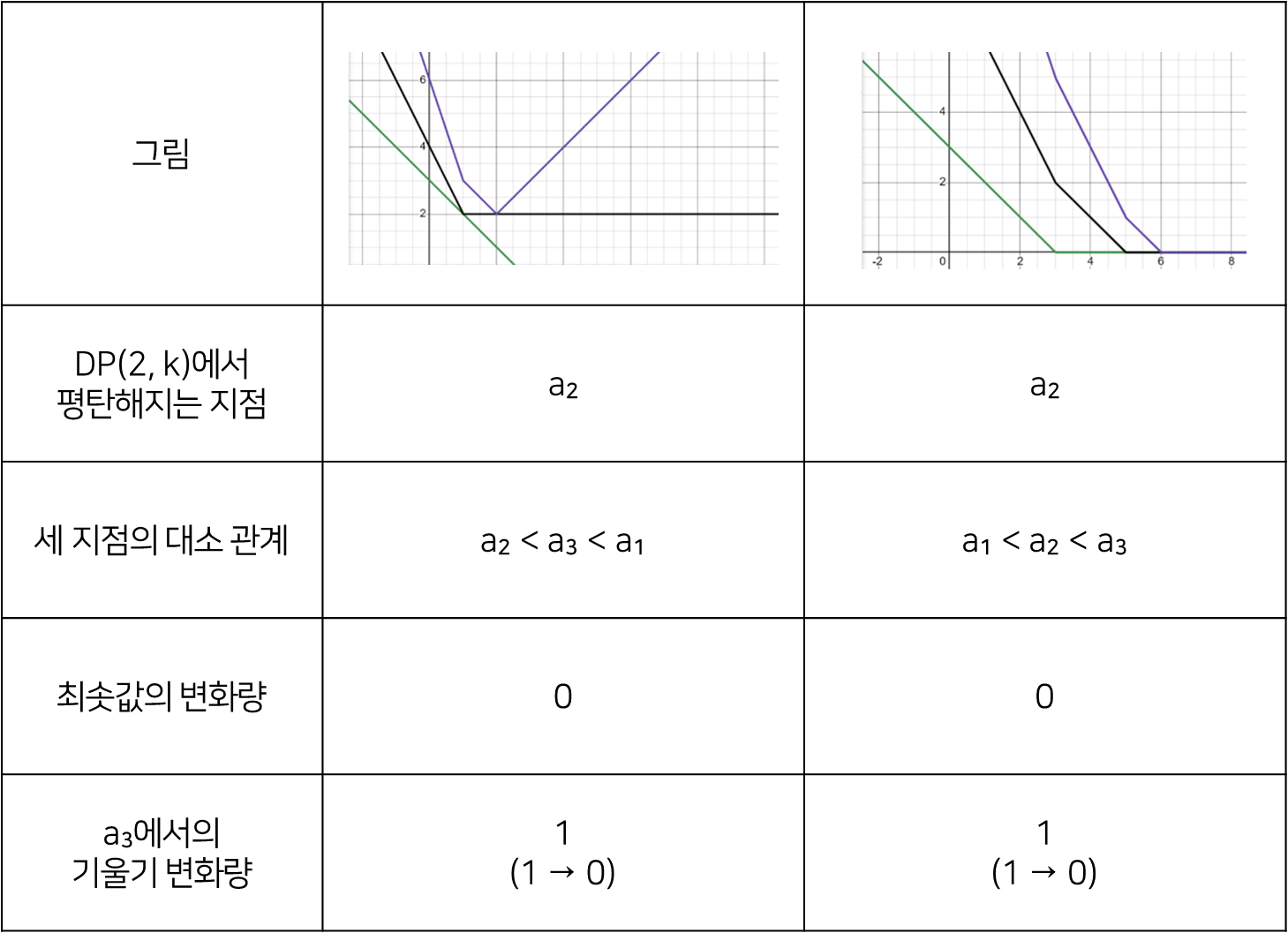
(중간에 보라색 그래프 위로 올라간 건 평평하다고 봐주세요)
두 지점의 대소 관계에 따라 서로 다른 특징이 나타나는 것을 알 수 있습니다.
따라서 해당 분석을 통해 얻을 수 있는 내용은 다음과 같이 정리할 수 있습니다.
- $DP(n-1, k)$에서 평탄해지는 지점 < $a_{n}$이면, 최솟값의 변화량은 없고 $a_{n}$에서 기울기는 1만큼 변한다.
- $DP(n-1, k)$에서 평탄해지는 지점 > $a_{n}$이면,
최솟값은 두 지점의 차의 절댓값만큼 변하고 $a_{n}$에서 기울기는 2만큼 변한다.
일반적으로 구하려고 하는 값은 최솟값입니다.
따라서, 최솟값의 변화량을 누적하여 더해주면 $DP(n, k)$에서의 최솟값을 구할 수 있게 됩니다.
두 지점의 차이를 누적해야 하므로 기울기가 변하는 여러 점들을 저장해야 하는 것은 분명합니다.
이때, 마지막으로 기울기가 변하는 지점부터는 평탄해지는 것이 자명하므로
마지막으로 기울기가 변하는 지점을 빠르게 구할 수 있어야 합니다.
즉 최댓값을 빠르게 구해야 하는 자료구조를 필요로 하는 것입니다.
이러한 경우에 딱 맞는 자료구조로 우선순위 큐가 있죠.
이때 기울기도 함께 관리해주기 위해서, 우선순위 큐에 있는 값에 대해서 각각
해당 지점을 기준으로 기울기 차이가 1이 난다는 것을 의미하도록 구성합니다.
이제 이를 구현해 봅시다.
구현은 정말 말도 안 될 정도로 간단하게 나타납니다.
위의 방식대로 우선순위 큐를 구현한다면, 식 $|a_{n} - x|$를 추가하는 것은 단순히 우선순위 큐에 $a_{n}$을 대입하는 것과 동치가 됩니다.
이때, 대입한 후 마지막 지점과 현재 지점이 동일하지 않다는 것은,
즉 pq.top() != $a_{n}$이라는 것은 평탄해지는 지점보다 왼쪽에 그래프가 위치함을 의미하게 되고,
이 경우 평탄해지는 지점 위로 기울기 1이 지나므로 평탄해지는 지점에서의 기울기 변화량은 0이 되게 됩니다.
또한 이때 $a_{n}$에서의 기울기 변화량은 2가 되게 되는데, 이는 단순히 pq.pop() 후 pq.push($a_{n}$)과 완전히 동일합니다.
아래는 맨 위에서 설명한 문제의 정답 코드입니다.
#include <iostream>
#include <queue>
using namespace std;
typedef long long int LL;
LL arr[1000001], res;
priority_queue<LL> pq;
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
int n;
cin >> n;
for(int i=0;i<n;i++) cin >> arr[i];
for(int i=0;i<n;i++)
{
LL cur = arr[i] - i;
pq.push(cur);
if(!pq.empty() && pq.top() > cur)
{
res += pq.top() - cur;
pq.pop();
pq.push(cur);
}
}
cout << res;
}'Problem Solving' 카테고리의 다른 글
| BOJ 2634. 버스노선 (1) | 2024.06.09 |
|---|---|
| BOJ 3295. 단방향 링크 네트워크 (0) | 2024.05.22 |
| Heavy-Light Decomposition (1) | 2024.05.21 |
| BOJ 28327. 지그재그 (0) | 2024.05.20 |
| 히르쉬버그 (Hirschberg) 알고리즘 (0) | 2024.04.03 |