Heavy-Light Decomposition이란 트리를 여러 개의 선형 구조로 분해하여 접근할 수 있게 해주는 기법입니다.
먼저 트리 위에서 다음과 같은 쿼리가 주어지는 문제를 생각해 봅시다.
- 정점 i의 가중치를 v로 변경한다.
- 두 정점 간의 경로 상의 정점의 가중치 합을 구한다.
당연히? $N \le 100000$ 정도입니다.
배열 위에서였다면 바로 신나게 세그먼트 트리를 짰겠지만, 트리 위이다 보니 바로 적용하기는 어렵습니다.
배열에서는 되고, 트리에서는 안 되는 이유는 무엇일까요?
당연한 소리지만, 트리는 배열과 달리 비선형구조이기 때문입니다.
그렇다면 이렇게, 트리를 여러 개의 선형 구조로 쪼갠다면 어떨까요?
이 경우에는 부분 부분에 대해서는 세그먼트 트리로 관리해줄 수 있겠다는 생각이 듭니다.
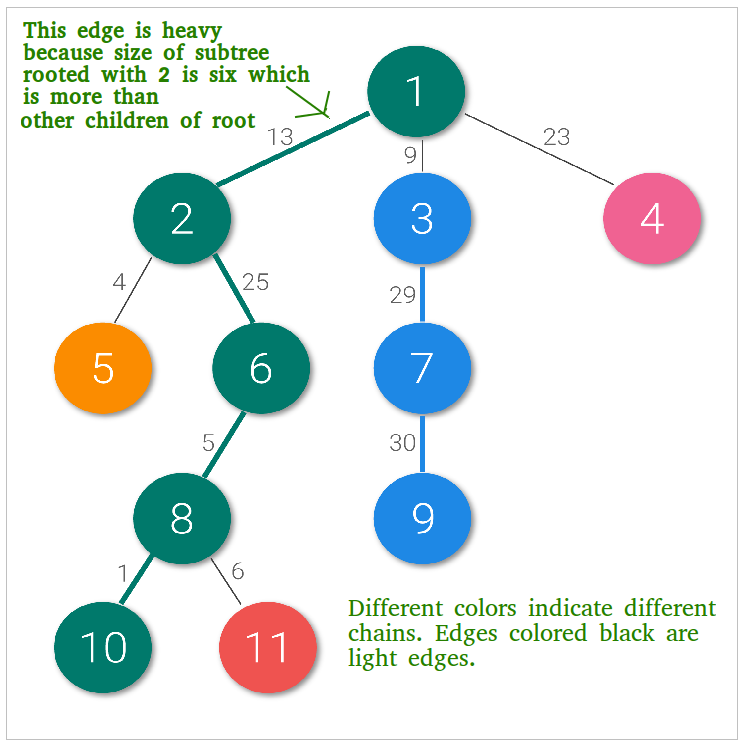
문제는 이걸 어떻게 쪼개서 만들 거냐는 것입니다.
냅다 쪼개면 운이 더럽게 없을 경우 그냥 일일이 확인하는 것만도 못할 정도로 느려터질 것입니다.
따라서 이를 똑똑하게 쪼개야 하고, 이 방법이 Heavy-Light Decompostion이 됩니다.
본격적으로 알아보기에 앞서, Heavy node과 Light node에 대한 정의가 필요합니다.
보통 다음 둘 중 하나의 조건을 정하고, 그 조건에 맞는 간선을 Heavy node,
그렇지 않은 간선을 Light node이라 합니다.
- 어떤 부모와 자식을 잇는 간선에 대해, 자식의 서브트리의 크기가 부모의 서브트리 크기의 절반 이상인 간선
- 어떤 부모에 대해, 자식들 중 서브트리의 크기가 가장 큰 자식을 연결하는 간선
이렇게 간선을 정의내리면 좋은 점은 여러 가지가 있습니다.
먼저 자명하다시피 어떤 부모와 그 자식들에 대하여 Heavy node는 하나밖에 없게 됩니다.
따라서 Heavy node로 연결된 노드들은 선형으로 관리해줄 수 있습니다.
(이때 이 연결된 노드들을 Heavy chain이라 합니다.)
또한 여기에서 미리 끝점을 기록해준다면 Heavy node의 맨 끝으로의 이동을 $O(1)$에 수행할 수 있습니다.
또한, 어떤 자식 노드에서 Light node을 통해 부모 노드로 올라간다면,
서브트리의 크기는 적어도 2배 이상이 됩니다.
따라서 Light node만 타고 올라간다면, 최대 $O(logN)$개의 간선만 타고도 루트 노드에 도달할 수 있습니다.
이제 구현을 해 봅시다.
먼저 dfs를 돌려서 자식 노드만 모아놓은 그래프를 만들어 줍시다.
void dfs(int cur, int prv)
{
for(auto nxt: node[cur]) //node: 양방향 그래프
{
if(nxt == prv) continue;
g[cur].push_back(nxt); //g: 자식만 모아놓은 그래프
dfs(nxt, cur);
}
}
다음으로 Heavy chain을 만들어 줍시다.
Heavy chain에서는 선형이여야 관리해줄 수 있기 때문에, 이를 연속적으로 나타낼 수 있도록 좀 뒤엎어 주어야 합니다.
대략적인 아이디어는 아래 그림과 같습니다.

적절히 서브트리의 크기를 기록해주며 바꿔 줍시다.
void hld(int cur) //cur: 현재 노드
{
sz[cur] = 1; //sz: 서브트리의 크기
/* swap 연산을 실행해 주어야 하므로 C++의 경우 레퍼런스로 탐색해야 함 */
for(auto &nxt: g[cur]) //g: 자식 노드만 모아놓은 그래프, nxt: 자식 노드
{
depth[nxt] = depth[cur] + 1; //depth: 깊이
parent[nxt] = cur; //parent: 닉값
hld(nxt); //DFS
sz[cur] += sz[nxt];
/* 현재 탐색한 자식 노드의 서브트리 크기가 가장 크다면 swap */
if(sz[nxt] > sz[g[cur][0]]) swap(nxt, g[cur][0]);
}
//탐색이 모두 끝나면 가장 먼저 탐색되는 자식 노드는 Heavy node가 됨
}
이제 DFS를 돌리며 번호를 매겨 줍시다.
이때 Heavy chain의 끝점도 관리해 주도록 하겠습니다.
int cnt = 1;
void ETT(int cur)
{
in[cur] = cnt++; //in: 번호
for(auto nxt: g[cur])
{
/* top[cur]: cur를 포함하는 Heavy chain 중 맨 위에 있는 점 */
/* 만약 Heavy node를 타고 내려왔다면 부모 정점과 동일, 그렇지 않으면 자기 자신부터 시작 */
top[nxt] = (nxt == g[cur][0] ? top[cur] : nxt);
ETT(nxt);
}
out[cur] = cnt - 1;
}
이제 쿼리를 처리해 봅시다.
Point Query의 경우 그냥 신나게 오일러투어 하듯이 접근해주면 되므로 Range Query에 대해서만 다루겠습니다.
트리의 성질에 의해, 트리 위의 임의의 서로 다른 두 정점에 대하여 이를 연결하는 경로는 유일합니다.
이전에 Heavy chain을 선형으로 다룰 수 있도록 잘 처리해 두었기 때문에,
해당 정점이 포함된 Heavy chain에서 빠르게 넘어가면서 탐색할 수 있습니다.
두 정점에서 LCA를 찾으려면 둘 다 계속해서 끌어올림으로써 만날 때까지 이를 반복했습니다.
비슷한 원리로, 두 점이 같은 Heavy-chain 상에 위치할 때까지 계속해서 끌어올려 줍니다.
이때 더 위에 있는 정점을 올리면 LCA를 지나쳐 버릴 수 있으므로
두 정점이 각각 속한 Heavy chain 중 끝점의 깊이가 깊은 것부터 끌어올려 줍니다.




보기 예시에서 처리할 구간은 [1, 4], [8, 10]이므로, 이는 쿼리 두번으로 처리가 가능합니다.
세그먼트 트리의 구현은 생략합니다.
int Query(int a, int b)
{
int res = 0;
while(top[a] != top[b]) //top: Heavy chain 끝점
{
if(depth[top[a]] < depth[top[b]]) swap(a, b); //a가 더 깊음
int st = top[a]; //a를 포함하는 heavy chain의 끝점
res += query(1, 1, n, in[st], in[a]); //쿼리 때리기
a = parent[st]; //끝점의 부모로 올라가기
}
/* 탐색 종료, 같은 Heavy chain에 위치 */
if(in[a] > in[b]) swap(a, b);
res += query(1, 1, n, in[a], in[b]); //쿼리 때리기
return res;
}
보통 간선에 대해서 처리를 해 주어야 할 때가 있는데,
이 경우 각각의 노드를 해당 노드를 통해 연결되는 자식 노드를 통해 관리해줌으로써 해결 가능합니다.
다만 이 경우 구간 처리를 살짝 유의해 주어야 합니다.
(위 코드의 경우 구간 쿼리를 [ in[st] + 1, in[a] ]로 때려 주어야 합니다. 한번 생각해 보면 이해할 수 있습니다.)
아래는 13510번: 트리와 쿼리 1 의 답안 코드입니다.
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
//Segment Tree
int n;
int tree[262144];
int upd(int node, int s, int e, int idx, int val)
{
if(idx < s || e < idx) return tree[node];
if(s == e) return tree[node] = val;
int m = (s + e) / 2;
int L = upd(node * 2, s, m, idx, val);
int R = upd(node * 2 + 1, m + 1, e, idx, val);
return tree[node] = max(L, R);
}
int que(int node, int s, int e, int l, int r)
{
if(r < s || e < l) return 0;
if(l <= s && e <= r) return tree[node];
int m = (s + e) / 2;
int L = que(node * 2, s, m, l, r);
int R = que(node * 2 + 1, m + 1, e, l, r);
return max(L, R);
}
int sz[101010], depth[101010], parent[101010], top[101010], in[101010], out[101010];
vector<int> node[100001], g[100001];
void dfs(int cur, int prv)
{
for(auto nxt: node[cur])
{
if(nxt == prv) continue;
g[cur].push_back(nxt);
dfs(nxt, cur);
}
}
void hld(int cur)
{
sz[cur] = 1;
for(auto &nxt: g[cur])
{
depth[nxt] = depth[cur] + 1;
parent[nxt] = cur;
hld(nxt);
sz[cur] += sz[nxt];
if(sz[nxt] > sz[g[cur][0]]) swap(nxt, g[cur][0]);
}
}
int cnt = 1;
void ETT(int cur)
{
in[cur] = cnt++;
for(auto nxt: g[cur])
{
top[nxt] = (nxt == g[cur][0] ? top[cur] : nxt);
ETT(nxt);
}
out[cur] = cnt - 1;
}
void update(int v, int w) { upd(1, 1, n, in[v], w); }
int query(int a, int b)
{
int res = 0;
while(top[a] != top[b])
{
if(depth[top[a]] < depth[top[b]]) swap(a, b);
int st = top[a];
res = max(res, que(1, 1, n, in[st], in[a]));
a = parent[st];
}
if(depth[a] > depth[b]) swap(a, b);
res = max(res, que(1, 1, n, in[a] + 1, in[b]));
return res;
}
struct edge
{
int p;
int q;
int w;
};
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cin >> n;
vector<edge> v(n);
for(int i=1;i<n;i++)
{
cin >> v[i].p >> v[i].q >> v[i].w;
node[v[i].p].push_back(v[i].q);
node[v[i].q].push_back(v[i].p);
}
dfs(1,0); hld(1); ETT(1);
for(int i=1;i<n;i++)
{
int &p = v[i].p, &q = v[i].q;
int w = v[i].w;
if(depth[p] < depth[q]) swap(p, q);
update(p, w);
}
int Q;
cin >> Q;
while(Q--)
{
int op;
cin >> op;
if(op == 1)
{
int i, w;
cin >> i >> w;
update(v[i].p, w);
}
if(op == 2)
{
int p,q;
cin >> p >> q;
cout << query(p, q) << '\n';
}
}
}
연습 문제
13510번: 트리와 쿼리 1 위에서 설명한 기본 문제입니다.
5916번: 농장 관리 Range Update 쿼리를 처리해야 하는 문제입니다. Range Query와 동일한 방식으로 처리할 수 있습니다.
2927번: 남극 탐험 빡구현을 해 봅시다.
'Problem Solving' 카테고리의 다른 글
| BOJ 2634. 버스노선 (1) | 2024.06.09 |
|---|---|
| BOJ 3295. 단방향 링크 네트워크 (0) | 2024.05.22 |
| BOJ 28327. 지그재그 (0) | 2024.05.20 |
| 함수 개형을 이용한 최적화 (Slope Trick) (0) | 2024.05.17 |
| 히르쉬버그 (Hirschberg) 알고리즘 (0) | 2024.04.03 |