DP를 활용하는 대표적인 문제로 LCS(Longest Common Sequence)가 있습니다.
시간복잡도 $O(N^{2})$, 공간복잡도 $O(N^{2})$로 해결하는 풀이가 가장 일반적입니다.

그렇다면 다음 문제를 봅시다.
https://www.acmicpc.net/problem/18438
18438번: LCS 5
LCS(Longest Common Subsequence, 최장 공통 부분 수열)문제는 두 수열이 주어졌을 때, 모두의 부분 수열이 되는 수열 중 가장 긴 것을 찾는 문제이다. 예를 들어, ACAYKP와 CAPCAK의 LCS는 ACAK가 된다.
www.acmicpc.net
문자열의 길이가 7000 이하이니 시간 복잡도는 문제될 게 없습니다만,
공간 복잡도가 비정상적으로 줄어버리며 난이도가 확 올라갔습니다.
공간 복잡도가 부족한 이유는 당연히 DP 테이블입니다.
단순 토글링으로 어찌저찌 길이는 구할 수 있겠으나, 역추적을 하기엔 무리가 있습니다.
히르쉬버그 알고리즘은 토글링을 기반으로 필요한 DP 테이블을 최소로 줄이는 방법입니다.
이렇게 하면 많아야 $O(N)$의 문자열만 남게 되므로, 공간 복잡도를 $O(N)$으로 줄일 수 있습니다.
다음과 같이 DP 테이블과 역추적에 필요한 결과가 담긴 그림을 확인해 봅시다.

분명한 건, 우리가 원하는 것은 파란색으로 칠해진 구간 뿐입니다.
바꿔 말하면 흰색으로 칠해진 부분은 결과에 전혀 필요 없게 됩니다.
따라서 이렇게 필요 없는 부분을 버릴 수 있습니다.
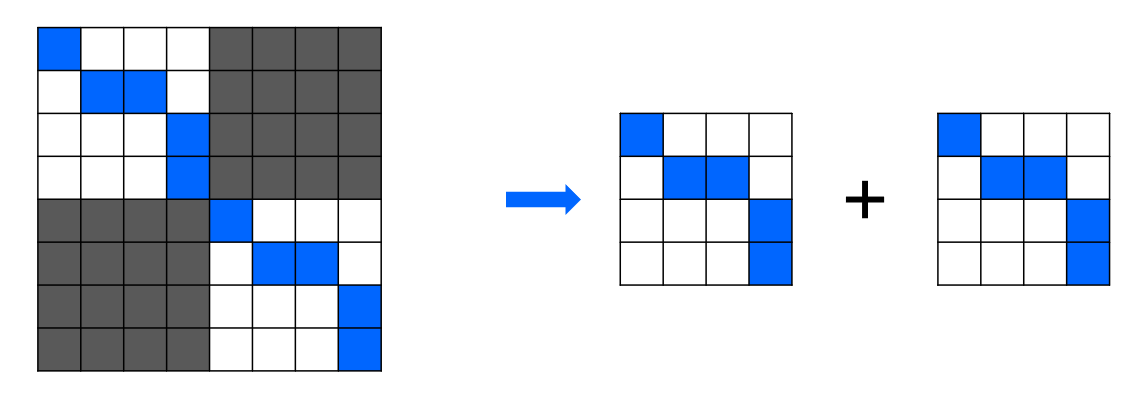
이때, 다음과 같이 쪼개진 두 문제는 처음에 구하려던 문제의 종류와 완전히 동일합니다.
따라서 이를 또 쪼개면 됩니다.
즉 분할 정복을 활용하여 이를 해결할 수 있습니다.
이제 코드를 구성해 봅시다.
먼저, 이렇게 쪼개진 문제들은 그냥 순서대로 이어 붙이면 LCS를 구할 수 있습니다.
이는 왼쪽 위부터 순서대로 내려가면 LCS가 구성되기 때문입니다.
따라서 쪼개고 쪼개다 행의 개수가 1이 된다면, 그냥 똑같은거 하나 얻어걸릴 때까지 계속 탐색하면 됩니다.
#include <iostream>
#include <string>
#include <vector>
using namespace std;
string a, b, res;
void LCS(int l1, int r1, int l2, int r2)
{
//LCS( a[l1 ~ r1], b[l2 ~ r2] )
if(l1 > r1) return;
if(l1 == r1)
{
for(int i=l2;i<=r2;i++)
{
if(a[l1] == b[i])
{
res.push_back(b[i]);
break;
}
}
return;
}
}
LCS 함수로 받는 매개변수는 현재 호출된 함수가 담당하는 구역입니다.
여기서는 구간이 [l1, r1]이라면 a[r1]도 포함되도록 구성하였습니다.
이제 구간이 적당히 클 경우 이를 분할 정복으로 해결할 수 있도록 구성해주어야 합니다.
먼저 DP 테이블을 구성해 줍시다.
길이만 구할 것이기 때문에, 토글링 기법을 활용하여 공간 복잡도 $O(2N)$으로 충분히 구할 수 있습니다.
이때, 분할 정복이므로 두 구간으로 쪼개고, 이를 다시 합치는 과정이 필요할 것입니다.
만약 두 구간 다 똑같이 위에서부터 쪼갠다면 아래와 같이 합치는 과정을 진행할 수 없습니다.
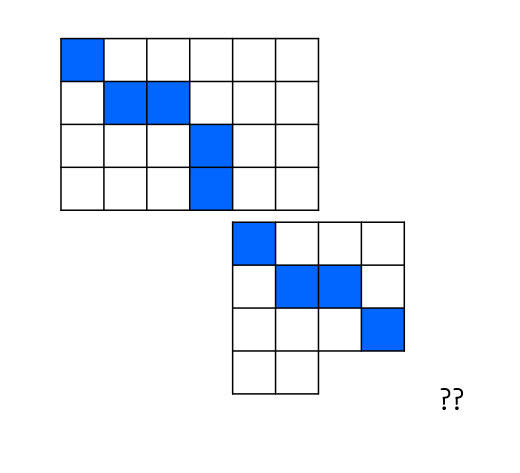
따라서 길이를 구할 때, 아래쪽에서 진행하는 LCS는 진행 방향을 반대로 구성해 주어야 합니다.
int m = (l1 + r1) / 2;
int len = (r2 - l2) + 1;
vector<int> up(len + 2), down(len + 2);
vector<int> prv(len + 2);
//위쪽 부분 DP
for(int i=l1; i<=m; i++)
{
for(int j=l2; j<=r2; j++)
{
if(a[i] == b[j]) up[j - l2 + 1] = prv[j - l2] + 1;
else up[j - l2 + 1] = max(up[j - l2], prv[j - l2 + 1]);
}
prv = up;
}
fill(prv.begin(), prv.end(), 0);
//아래쪽 부분 DP
for(int i=r1; i>m; i--)
{
for(int j=r2; j>=l2; j--)
{
if(a[i] == b[j]) down[j - l2 + 1] = prv[j - l2 + 2] + 1;
else down[j - l2 + 1] = max(down[j - l2 + 2], prv[j - l2 + 1]);
}
prv = down;
}
이렇게 각각 DP를 실행했다면, DP 배열에는 (한 문자열 전체와 다른 문자열의 부분에 대한 LCS 길이)
가 담겨 있을 것입니다.
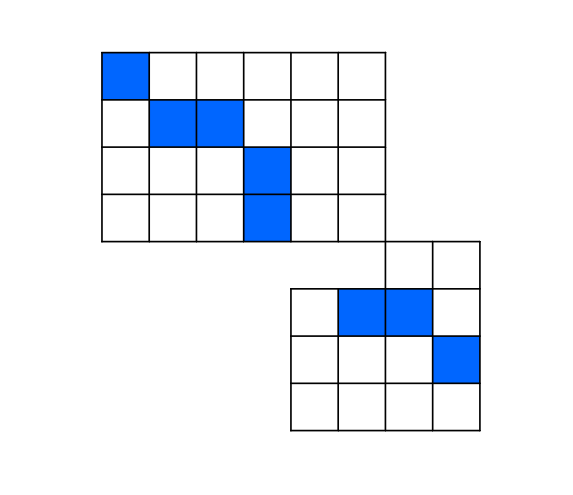
만약 아래처럼 바보같이 합치면 지금까지 해왔던 게 다 뻘짓이 될 것입니다.

따라서, 구간을 합치는 경우 중 LCS가 가장 긴 경우를 골라서 분할해 주어야 LCS를 구할 수 있습니다.
이는 미리 구해놓은 DP 배열을 활용하여 탐색하면 됩니다.
int mx = -1, idx = 0;
for(int i=l2; i<=r2 + 1; i++)
{
if(mx < up[i - l2] + down[i - l2 + 1])
{
mx = up[i - l2] + down[i - l2 + 1];
idx = i;
}
}
마지막으로 재귀호출을 할 때에도 범위를 잘 정해 주어야 합니다.
현재 설명하고 있는 코드를 예시로 들면, 구해놓은 DP의 정의는 다음과 같습니다.
DP[i]: i-1번째 원소까지 포함하였을 때의 LCS
따라서 구간을 [l2, idx-1], [idx, r2]로 나누어 주어야 할 것입니다.
이 과정을 거쳤다면 res 배열에는 LCS 문자열이 잘 저장되어 있을 것이므로 이를 출력하면 문제를 해결할 수 있습니다.
아래는 전체 풀이입니다.
#include <iostream>
#include <string>
#include <vector>
using namespace std;
string a, b, res;
void LCS(int l1, int r1, int l2, int r2)
{
//LCS( a[l1 ~ r1], b[l2 ~ r2] )
if(l1 > r1) return;
if(l1 == r1)
{
for(int i=l2;i<=r2;i++)
{
if(a[l1] == b[i])
{
res.push_back(b[i]);
break;
}
}
return;
}
int m = (l1 + r1) / 2;
int len = (r2 - l2) + 1;
vector<int> up(len + 2), down(len + 2);
vector<int> prv(len + 2);
//위쪽 부분 DP
for(int i=l1; i<=m; i++)
{
for(int j=l2; j<=r2; j++)
{
if(a[i] == b[j]) up[j - l2 + 1] = prv[j - l2] + 1;
else up[j - l2 + 1] = max(up[j - l2], prv[j - l2 + 1]);
}
prv = up;
}
fill(prv.begin(), prv.end(), 0);
//아래쪽 부분 DP
for(int i=r1; i>m; i--)
{
for(int j=r2; j>=l2; j--)
{
if(a[i] == b[j]) down[j - l2 + 1] = prv[j - l2 + 2] + 1;
else down[j - l2 + 1] = max(down[j - l2 + 2], prv[j - l2 + 1]);
}
prv = down;
}
int mx = -1, idx = 0;
for(int i=l2; i<=r2 + 1; i++)
{
if(mx < up[i - l2] + down[i - l2 + 1])
{
mx = up[i - l2] + down[i - l2 + 1];
idx = i;
}
}
LCS(l1, m, l2, idx-1);
LCS(m+1, r1, idx, r2);
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cin >> a >> b;
LCS(0, a.size() - 1, 0, b.size() - 1);
cout << res.size() << '\n' << res;
}'Problem Solving' 카테고리의 다른 글
| BOJ 2634. 버스노선 (1) | 2024.06.09 |
|---|---|
| BOJ 3295. 단방향 링크 네트워크 (0) | 2024.05.22 |
| Heavy-Light Decomposition (1) | 2024.05.21 |
| BOJ 28327. 지그재그 (0) | 2024.05.20 |
| 함수 개형을 이용한 최적화 (Slope Trick) (0) | 2024.05.17 |