간단히 말해 트라이 위에서 KMP를 수행하는 알고리즘이다.
짤막하게 트라이와 KMP를 짚어보고 넘어가겠다.
1. 트라이(Trie)
N개의 길이 M 문자열 리스트가 있을 때, 어떤 문자열이 해당 리스트에 포함되어 있는 지 판단하는 알고리즘을 짠다고 하자.
Naive하게 짜면 $O(NM)$일 것이고, 여기서 더 줄일 수 있는 방법은 딱히 없어 보인다.
(정렬을 하면 $O(MlogN)$으로 줄어들긴 하겠지만, 그 과정이 애초에 비효율적이다.)
트라이는 트리 자료구조에서 착안하여, 무려 $O(M)$에 찾을 수 있도록 구성해준 것이다.
기본적으로 다음과 같이, 트리를 따라 리프 노드까지 쭉 따라가면서 순서대로 합친 것을 문자열로 생각한다.
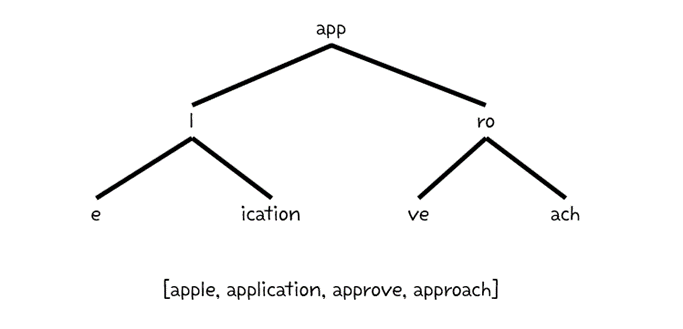
보통 포인터를 활용하여 구성한다. 아래는 트라이 코드의 일부이다.
struct node
{
node* c[26]; //자식노드
int cnt; //자식노드 개수
bool fin; //단어의 끝 성분인가
node()
{
for(int i=0;i<26;i++) c[i]=NULL;
cnt=0; fin=false;
}
~node()
{
for(int i=0;i<26;i++) if(c[i]!=NULL) delete c[i];
}
void insert(string &s, int idx)
{
if(idx==s.length()) //더 이상 넣을 문자가 없다(현재 노드가 단어의 끝)
{
fin=true;
return;
}
if(c[s[idx]-'a']==NULL)
{
c[s[idx]-'a']=new node();
cnt++;
}
c[s[idx]-'a']->insert(s,idx+1);
}
};
2. KMP 알고리즘
어떤 문자열이 다른 문자열의 부분 문자열인 지를 $O(N+M)$에 탐색할 수 있도록 하는 알고리즘이다.
실패 함수라는 개념이 필요한데, 각각의 접두사 문자열에 대해 접두사와 접미사가 같아지는 최대 길이(전체 빼고)를 기록한다.

이걸 구해 놓으면 매칭을 쭉 돌리다 실패했을 때 많은 작업을 건너뛸 수 있게 해준다.
대충 이러한 탐색 과정을 가지고 있다고 해보자.

이때 무식하게 한 칸만 옮기는 게 아니라, 미리 구해놓은 실패함수를 이용해 이렇게 확 건너뛸 수 있다.

아래는 본인이 사용하는 KMP 템플릿이다. 아무래도 메인 주제는 아닌 만큼 대충 넘어가겠다.
#include <iostream>
#include <string>
#include <vector>
using namespace std;
/* KMP Template, returns matching prefix index vector */
vector<int> KMP(string str, string substr)
{
const int len = str.length();
const int sublen = substr.length();
vector<int> res;
/* Construct Failure Function */
vector<int> pi(sublen);
int prefix = 0;
for(int suffix = 1; suffix < sublen; suffix++)
{
while(prefix > 0 && substr[prefix] != substr[suffix]) prefix = pi[prefix - 1];
if(substr[prefix] == substr[suffix]) pi[suffix] = ++prefix;
}
/* Find */
int sub_idx = 0;
for(int str_idx = 0; str_idx < len; str_idx++)
{
while(sub_idx > 0 && str[str_idx] != substr[sub_idx]) sub_idx = pi[sub_idx - 1];
if(str[str_idx] == substr[sub_idx])
{
sub_idx++;
if(sub_idx == sublen)
{
res.push_back(str_idx - (sublen - 1));
sub_idx = pi[sub_idx - 1];
}
}
}
return res;
}여기까지가, 배경지식이다. BFS도 필요하긴 한데 솔직히 이거 할 정도면 당연히 알 거라 생각한다.
3. 아호-코라식 (Aho-Corasick)
요약하면 이 두개를 짬뽕시킨 것이다.
실제로 트라이 위에서 하는 실패함수 구축 과정이 KMP와 거의 동일하다.
여기서는 KMP를 알고 있다는 전제 하에 글을 작성한다. 설명하기 어렵기도 하고.
먼저, 실패함수를 구축하려면 현재 탐색 중인 노드의 모든 조상들에 대해 이미 실패함수가 구축되어 있어야 한다.
이는 트라이 탐색을 너비 우선 탐색으로 함으로써 간단히 해결된다.
어떤 한 노드에 대해서, 계속 부모 노드를 타고 올라가 얻은 문자열에 대해 KMP를 수행한다고 하자.
아래 트리를 예시로 들어 보자.

먼저 부모 노드가 루트라면, 그 노드의 실패함수는 루트 노드이다. 실패함수의 정의에 의해, 1글자일 경우 실패함수는 항상 0이다.

A의 자식노드 B에 대하여 현재까지의 문자열은 AB이다. 마찬가지로 실패함수는 루트 노드로 간다.
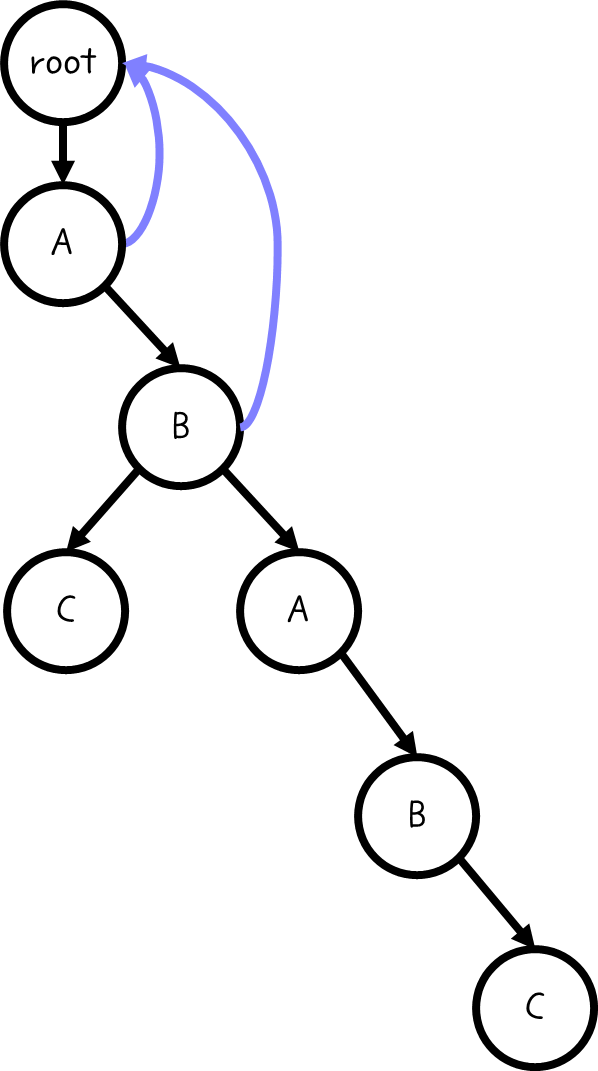
마찬가지로 ABC의 경우 C의 실패함수는 루트 노드이다. 중요한 점은 ABA이다.
ABA의 경우 접두사와 접미사가 일치하는 구간이 존재한다.(A)
이 경우, KMP 짜듯이 실패함수를 다음과 같이 구축해 준다.
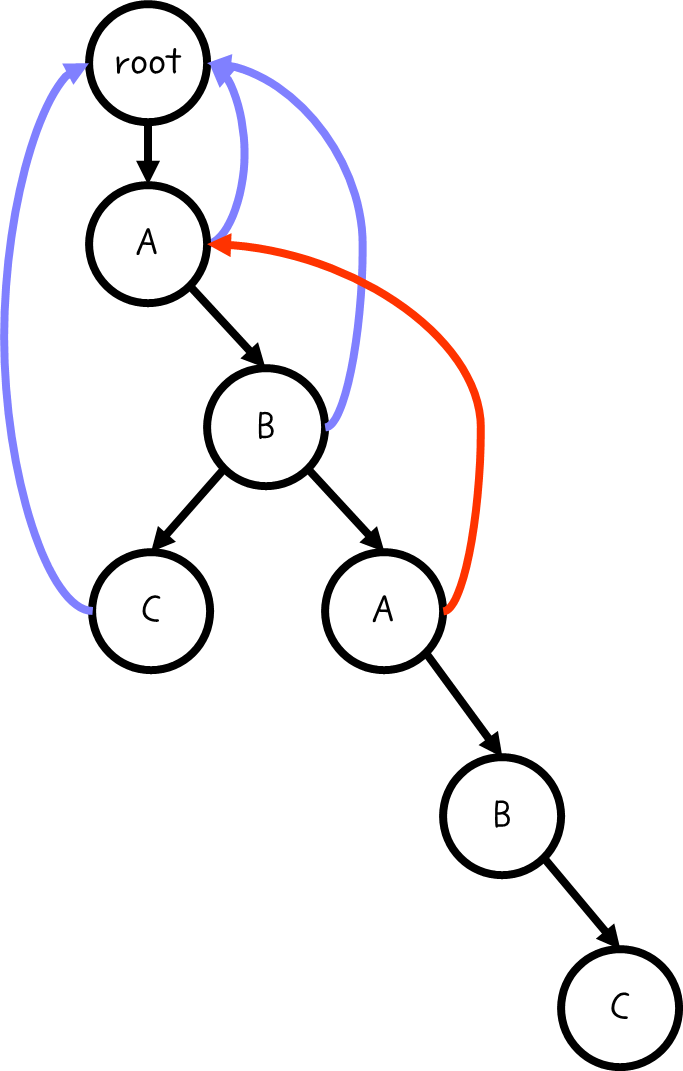
ABAB의 경우 처음 B로 이동하게 될 것이다.
이제 ABABC의 경우가 중요하다. 바로 앞인 ABAB의 실패함수를 따라가면, AB에 도달하게 될 것이다.
이때 위의 AB에도 C가 있고, ABAB에도 C가 있으므로 공통적으로 ABC를 매칭시켜줄 수 있다.
따라서 실패함수는 다음과 같이 구축된다.
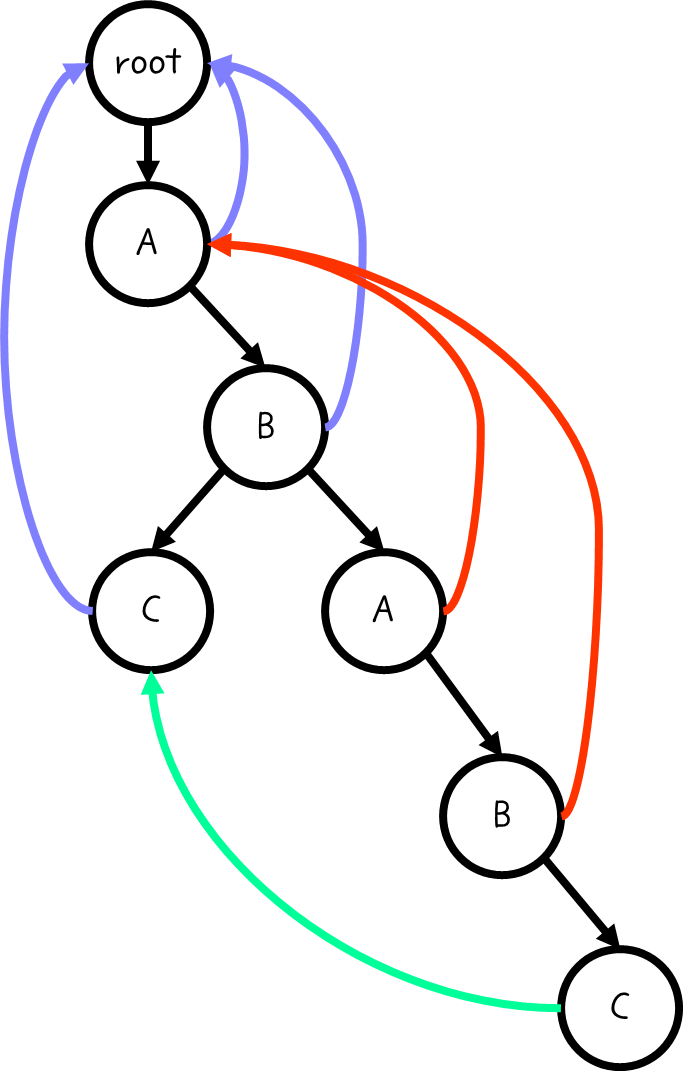
따라가 보면 알 수 있듯, KMP와 사실상 동일한 방법으로 실패함수를 구성한다.
사실 매칭도 KMP와 동일한 방법이라, 설명은 코드로 대체한다.
void AhoCorasick()
{
queue<Trie*> q;
root -> fail = root;
q.push(root);
while(!q.empty())
{
Trie* cur = q.front();
q.pop();
for(int i = 0; i < 26; i++)
{
Trie* nxt = cur -> go[i];
if(!nxt) continue;
if(cur == root) nxt -> fail = root; //fail(root) = root
else
{
Trie* dest = cur -> fail;
while(dest != root && !(dest -> go[i])) dest = dest -> fail;
if(dest -> go[i] != nullptr) dest = dest -> go[i];
nxt -> fail = dest;
}
if(nxt -> fail -> output) nxt -> output = true;
q.push(nxt);
}
}
}
bool TrieMatch(string str)
{
Trie* cur = root;
bool res = false;
for(int i = 0; i < str.length(); i++)
{
int nxt = str[i] - 'a';
while(cur != root && !(cur -> go[nxt])) cur = cur -> fail;
if(cur -> go[nxt]) cur = cur -> go[nxt];
if(cur -> output)
{
res = true;
break;
}
}
return res;
}
중요하게 보아야 할 것은 output 변수의 관리이다.
여기서는 해당 노드를 끝으로 하는 문자열이 존재하는지를 판별해 주는 변수이다.
위의 예시에서는 다음과 같이 색칠된 노드에 output 변수가 true로 되어 있을 것이다.
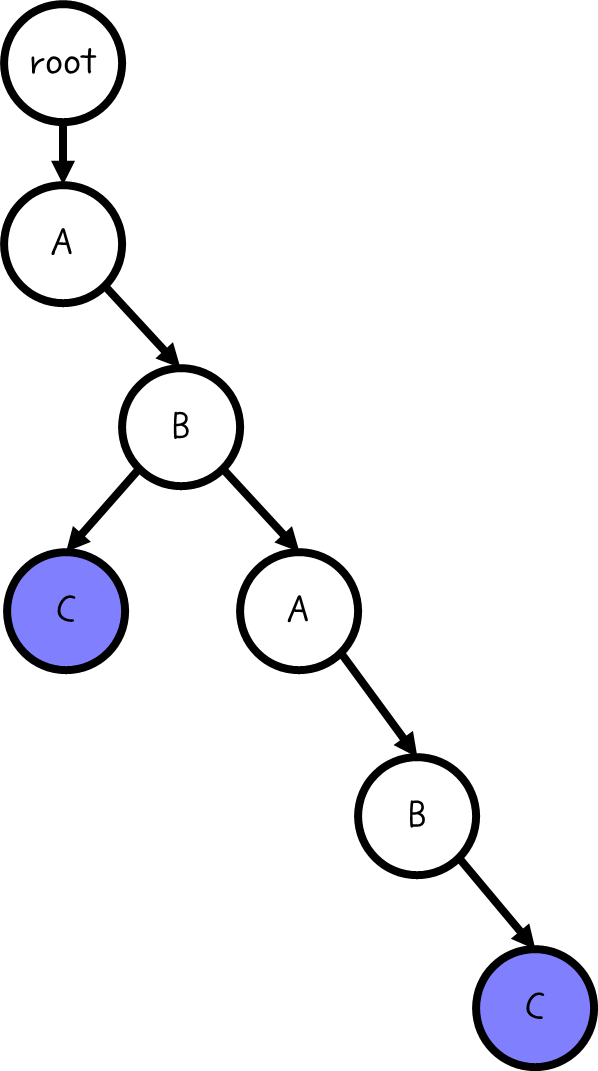
여기서 만약 AB라는 변수가 추가되었다고 해 보자.
그러면 일단 이렇게 색칠이 되어 있을 것이다.
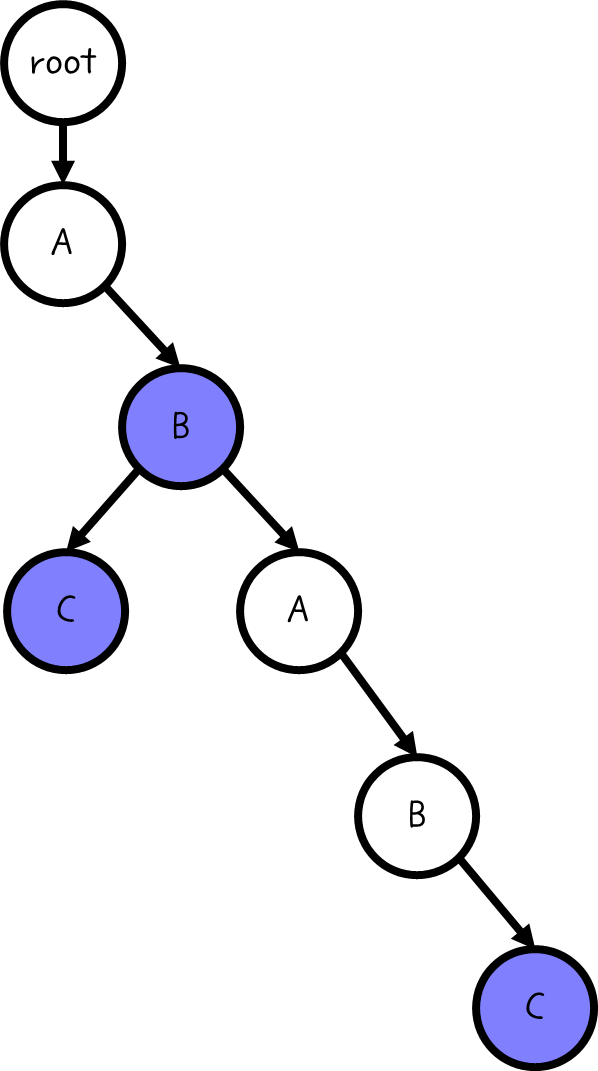
만약, 여기 초록색으로 색칠된 부분을 탐색 중이라고 해 보자.
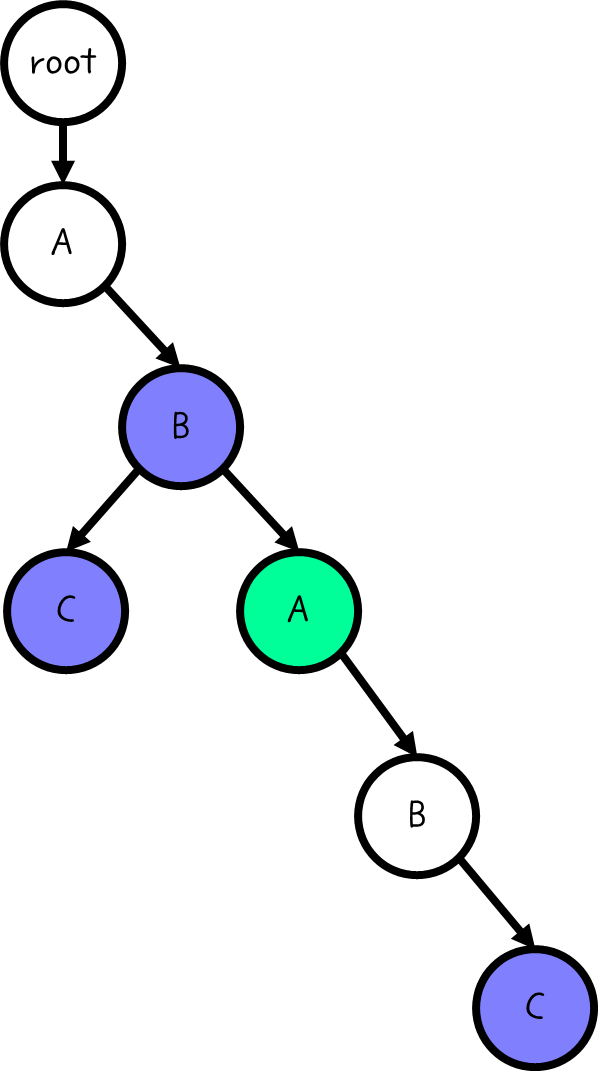
여기서부터 내려간다면, 돌아가지 않는 이상 "AB"라는 문자열은 존재하는 지 판별할 수 없다. 적어도 이렇게 색칠되어 있다면.
그런데 우리는 이렇게 AB가 존재하는 것을 알고 있다. 이 점을 해결해 주어야 한다.
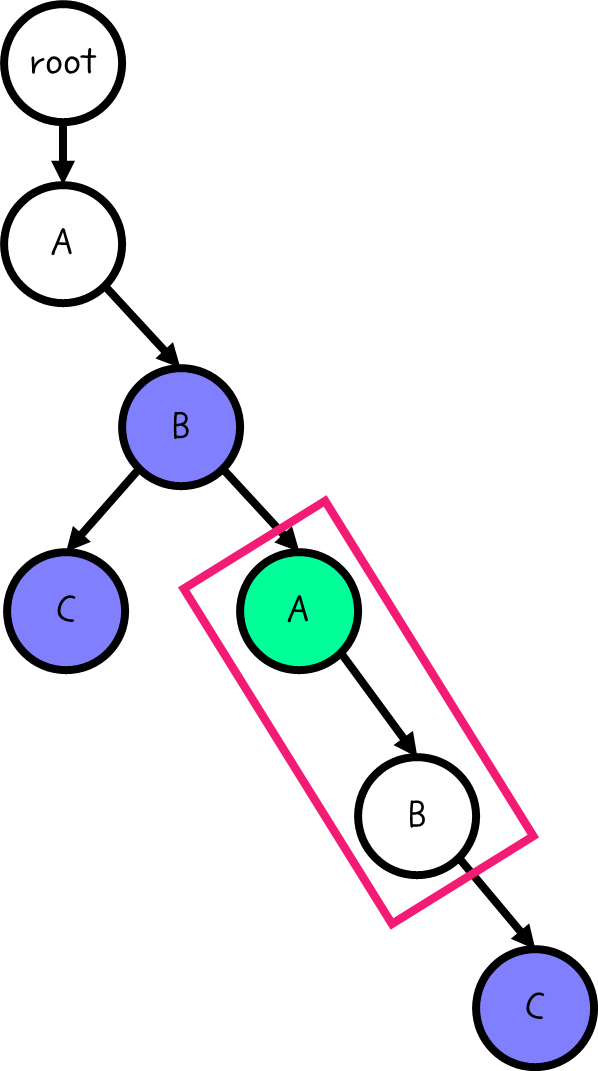
아호-코라식의 경우 문자열 끝만 마킹하지 않고, 일단 해당 지점을 끝으로 하는 문자열이 포함될 수 있다면 모두 마킹한다.
잠시 실패함수의 정의를 생각해보면, 해당 노드를 마지막으로 하는 문자열에 대해서,
가장 길고 겹치는 접두사와 접미사에 대해 접두사의 맨 끝으로 이동한다.
근데 접두사가 마킹이 되어 있다면? 접미사도 겹치므로 해당 노드를 끝으로 하는 부분 문자열도 반드시 존재한다는 것이다.
그래서 BFS 탐색이 끝나고, 다음과 같은 과정이 추가로 들어가는 것이다.
if(nxt -> fail -> output) nxt -> output = true;
아래는 아호코라식 기초 구현의 예제들이다.
9250번: 문자열 집합 판별 (acmicpc.net)
'Problem Solving' 카테고리의 다른 글
| BOJ 11012. Egg (0) | 2024.08.26 |
|---|---|
| BOJ 7626. 직사각형 (0) | 2024.08.26 |
| BOJ 3665. 최종 순위 (0) | 2024.08.23 |
| BOJ 1450. 냅색문제 (0) | 2024.08.22 |
| BOJ 13896. Sky Tax (0) | 2024.08.13 |